Cho tam giác ABC, vẽ ra ngoài tam giác các đoạn thẳng AM, AN sao cho
MAB=ABC; NAC=ACB . Chứng tỏ rằng M, A, N thẳng hàng
giúp mk với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 1 2016
cho tam giác abc óoác a nhọn vẽ ra ngoài tam giac abo các goc BAX và CAI SAO CHO 2 GÓC = 3O độ . trên tia Ax lấy điểm m , trên tia AI sao cho am=ab,an=ac
10 tháng 8 2016
B C A M N
Ta có
AM//BC => ABC=BAM
AN//BC => ACB=CAN
Do đó
ABC+ACB+BAC=BAM+CAN+BAC=180
Vậy ba điểm A,M,N thẳng hàng
2 tháng 3 2023
`a)`
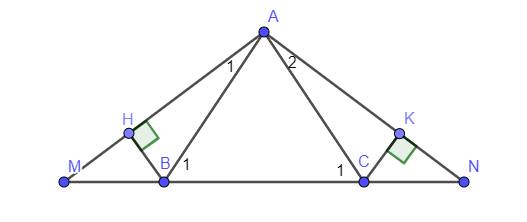
Có `Delta ABC` cân tại `A=>hat(B_1)=hat(C_1);AB=AC`
Có `hat(B_1)+hat(ABM)=180^0` ( kề bù )
`hat(C_1)+hat(ACN)=180^0` (kề bù)
mà `hat(B_1)=hat(C_1)(cmt)`
nên `hat(ABM)=hat(ACN)`
Xét `Delta ABM` và `Delta ACN` có :
`AB=C(cmt)`
`hat(ABM)=hat(ACN)(cmt)`
`BM=CN(GT)`
`=>Delta ABM=Delta ACN(c.g.c)(đpcm)`
`b)`
Có `Delta ABM=Delta ACN(cmt)=>hat(A_1)=hat(A_2)` ( 2 góc t/ứng )
Xét `Delta AHB` và `Delta AKC` có :
`hat(AHB)=hat(AHC)(=90^0)`
`AB=AC(cmt)`
`hat(A_1)=hat(A_2)(cmt)`
`=>Delta AHB=Delta AKC(c.h-g.n)(đpcm)`
NH
14 tháng 2 2020
ABCNM
a ) Xét tam giác AMB và tam giác NMC có :
AM = MN ( gt )
Góc AMB = góc NMC ( đối đỉnh )
BM = MC ( vì AM là đường trung tuyến của BC )
=> Tam giác AMB = Tam giác NMC ( c.g.c )
=> Góc ABM = góc NCM ( 2 góc tương ứng )
Mà góc ABM = góc NCM so le trong
=> CN // AB
b ) Xét tam giác ABC và tam giác NCB có :
AB = NC ( tam giác AMB = tam giác NMC mà cạnh AB và NC là 2 cạnh tương ứng )
Góc ABC = góc NCB ( vì tam giác AMB = tam giác NMC mà góc ABC và góc NCB là 2 góc tương ứng )
AB là cạnh chung
=> Tam giác ABC = Tam giác NCB ( c.g.c )
mk ko cần nữa đâu