so sánh :
A=1+2+2²+2³+.......+2⁶⁰ và b= 2⁶¹
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
4
24 tháng 10 2021
\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)
AM
28 tháng 6 2015
\(A=1+\frac{1}{2}+...+\frac{1}{2^{100}}\)
=>\(2A=2+1+\frac{1}{2}+...+\frac{1}{2^{99}}\)
=>2A-A=\(\left(2+1+\frac{1}{2}+...+\frac{1}{2^{99}}\right)-\left(1+\frac{1}{2}+...+\frac{1}{2^{100}}\right)=2-\frac{1}{2^{100}}<2\)
Vậy A<B
28 tháng 6 2015
=> \(\frac{1}{2}\)A = \(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{101}}\)
=> A - \(\frac{1}{2}\) A = \(\frac{1}{2}\)A = \(\frac{1}{2^{101}}-1\)
=> A = \(\frac{\frac{1}{2^{101}}-1}{2}=\frac{\frac{1}{2^{101}}}{2}-\frac{1}{2}=\frac{1}{2^{102}}-\frac{1}{2}<1<2\)
=> A < B
DH
2
14 tháng 9 2023
`# \text {DNamNgV}`
\(A=1+2+2^2+...+2^{2021}\text{ và }B=2^{2022}\)
Ta có:
\(A=1+2+2^2+...+2^{2021}\\ \Rightarrow2A=2+2^2+2^3+...+2^{2022}\\\Rightarrow2A-A=\left(2+2^2+2^3+...+2^{2022}\right)-\left(1+2+2^2+...+2^{2021}\right)\\ \Rightarrow A=2+2^2+2^3+...+2^{2022}-1-2-2^2-...-2^{2021}\\ \Rightarrow A=2^{2022}-1\)
Vì \(2^{2022}-1< 2^{2022}\)
\(\Rightarrow A< B.\)
TN
1
13 tháng 8 2021
Ta có: \(A=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1< 2^{32}\)
\(\Leftrightarrow A< B\)
AT
1
J
1
12 tháng 4 2019
= 1/2.2 + 1/3.3 + ... + 1/2018.2018
= ( 1/2 - 1/2) + (1/3 - 1/3) + ... + ( 1/2018 - 1/2018 )
= 0+0+0+0+...+0
=0
75% = 7,5
7,5 > 0 ==>
A<B
F
2
XO
11 tháng 6 2020
B = 75% => B = 3/4
Ta có :\(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{2018^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2017.2018}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2017}-\frac{1}{2018}=1-\frac{1}{2018}\)
Vì \(\frac{1}{2018}< \frac{1}{4}\Rightarrow1-\frac{1}{2018}>1-\frac{1}{4}\Rightarrow A>\frac{3}{4}\)=> A > B
F
11 tháng 6 2020
\(A=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{2018^2}\)
\(B=75\%=\frac{3}{4}\)
Ta có:\(A=.......\)
\(=\frac{1}{4}+\left(\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{2018^2}\right)< \frac{1}{4}+\left(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2017.2018}\right)\)
\(=\frac{1}{4}+\frac{1}{2}-\frac{1}{2018}=\frac{3}{4}-\frac{1}{2018}< \frac{3}{4}\)
\(\Rightarrow A< B\)
M
2
B
11 tháng 5 2019
A = 1 + 2 + 22 + 23 + ... + 22002
=> 2A = 2 + 22 + 23 + 24 + ... + 22003
=> 2A - A = ( 2 + 22 + 23 + 24 + ... + 22003 ) - ( 1 + 2 + 22 + 23 + ... + 22002 )
A = 22003 - 1 < 22003
hay A < B
Vậy ...
11 tháng 5 2019
\(A=1+2+2^2+2^3+...+2^{2002}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{2002}+2^{2003}\)
\(\Rightarrow2A-A=2^{2003}-1\)
\(\Rightarrow A=2^{2003}-1\)
Vì \(2^{2003}-1< 2^{2003}\)
nên A < B
NH
1
HP
21 tháng 9 2015
A = 1+ 2+ 2^2 + ..... + 2^ 2009
2A = 2 + 2^2 + .... + 2^2010
2A - A = 2^2010 - 1 = A
B = 2^ 2010 - 1
=> A = B
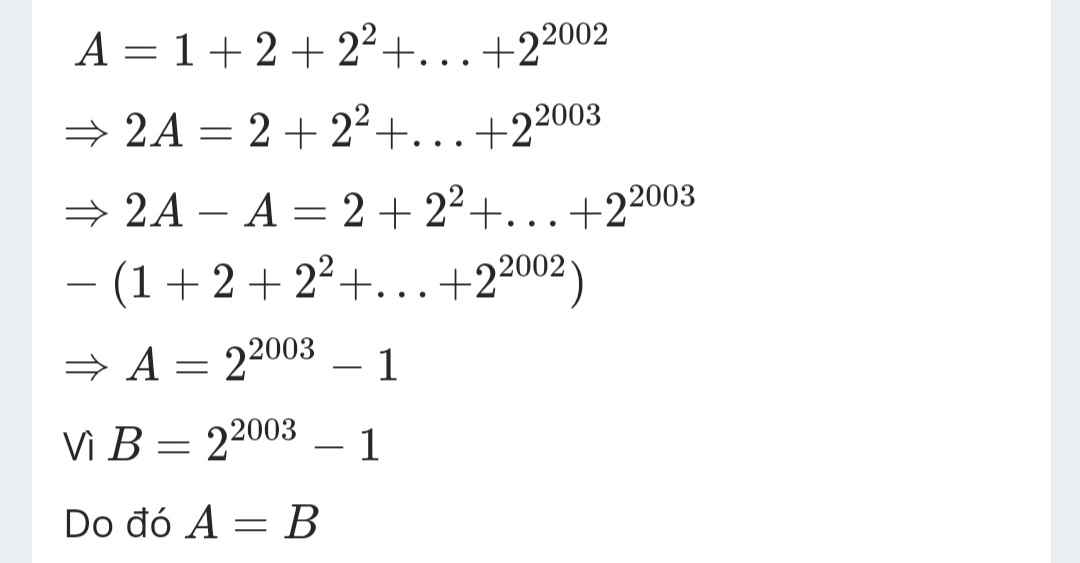
\(A=1+2+2^2+2^3+...+2^{60}\)
\(A+1=1+1+2+2^2+2^3+...+2^{60}\)
\(A+1=2+2+2^2+2^3+...+2^{60}\)
\(A+1=2^2+2^2+2^3+...+2^{60}\) ( 2 số giống nhau thì tổng bằng số đó nhân đôi đồng nghĩa với việc số mũ của nó sẽ tăng 1 )
\(A+1=2^3+2^3+...+2^{60}\)
\(A+1=2^{61}\)
\(A=2^{61}-1\)
Vậy A < B