Cho M,N lần lượt là trung điểm AB,.CD. Chứng minh rừng:
Vecto AC+vecto BD= 2 Vecto MN
Mn ơi giúp e vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
2 tháng 9 2021
xét tam giác ABD có:
M là trung điểm AB
Q là trung điểm AD
suy ra MQ là đường trung bình của tam giác ABD
suy ra MQ // BD, MQ = 1/2.BD (1)
xét tam giác BCD có:
N là trung điểm BC
P là trung điểm DC
suy ra NP là đường trung bình của tam giác BCD
suy ra NP//BD, NP = 1/2.BD (2)
từ (1), (2) suy ra NP//MQ và NP = MQ
suy ra vecto NP = MQ
chứng minh tương tự trên thì ta cũng được vecto NM = PQ
M là trung điểm AB
Q là trung điểm AD
suy ra MQ là đường trung bình của tam giác ABD
suy ra MQ // BD, MQ = 1/2.BD (1)
xét tam giác BCD có:
N là trung điểm BC
P là trung điểm DC
suy ra NP là đường trung bình của tam giác BCD
suy ra NP//BD, NP = 1/2.BD (2)
từ (1), (2) suy ra NP//MQ và NP = MQ
suy ra vecto NP = MQ
chứng minh tương tự trên thì ta cũng được vecto NM = PQ
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
Ta có M là trung điểm AB, N là trung điểm BC
\(\Rightarrow\) MN là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\)
Hoàn toàn tương tự, PQ là đường trung bình tam giác ACD
\(\Rightarrow\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{MN}=\overrightarrow{QP}\)
13 tháng 10 2021
a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
\(\overrightarrow{NC}=2\overrightarrow{ND}=2\overrightarrow{NC}+2\overrightarrow{CD}\Rightarrow\overrightarrow{NC}=2\overrightarrow{DC}\Rightarrow\overrightarrow{CN}=2\overrightarrow{CD}\)
a.
\(\overrightarrow{DM}=\overrightarrow{DC}+\overrightarrow{CM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{CD}=-2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\\\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MN}=-2\left(\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\right)=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{5}{4}\overrightarrow{BD}\)
CM
5 tháng 8 2018
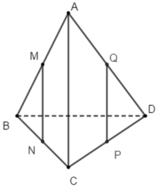
Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC và
M
N
=
1
2
A
C
(1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và Q P = 1 2 A C (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)
Đáp án C
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 9 2019
Do MN là đường trung bình hình thang nên \(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{DC}\right)\)
Mà \(CD=2AB\Rightarrow\overrightarrow{DC}=2\overrightarrow{AB}\Rightarrow\overrightarrow{MN}=\frac{3}{2}\overrightarrow{AB}\)
Ta có: \(\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}=\frac{3}{2}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{CB}+\overrightarrow{BA}\)
\(=\frac{3}{2}\overrightarrow{AB}-\overrightarrow{DC}-\overrightarrow{AB}=\frac{3}{2}\overrightarrow{AB}-2\overrightarrow{AB}-\overrightarrow{AB}=-\frac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\left|\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}\right|=\left|-\frac{3}{2}\overrightarrow{AB}\right|=\frac{3}{2}AB=\frac{3a}{2}\)
\(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NC}+\overrightarrow{BM}+\overrightarrow{MN}+\overrightarrow{ND}\)
\(=2\overrightarrow{MN}+\left(\overrightarrow{AM}+\overrightarrow{BM}\right)+\left(\overrightarrow{NC}+\overrightarrow{ND}\right)=2\overrightarrow{MN}\)