Trình bày chi tiết
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=\dfrac{10^7-8+13}{10^7-8}=1+\dfrac{13}{10^7-8}\)
\(B=\dfrac{10^8-7+13}{10^8-7}=1+\dfrac{13}{10^8-7}\)
mà \(10^7-8< 10^7-7< 10^8-7\)
nên A>B

\(A=\dfrac{-19}{9}\left(\dfrac{1}{2}-\dfrac{4}{11}\right)+\dfrac{-2}{3}=\dfrac{-19}{9}\cdot\dfrac{3}{22}+\dfrac{-2}{3}=\dfrac{-21}{22}\)
\(B=\dfrac{15}{6}\cdot2-\dfrac{7}{12}+\dfrac{1}{3}\cdot\dfrac{11}{2}=\dfrac{15}{3}-\dfrac{7}{12}+\dfrac{11}{6}\)
\(=\dfrac{60}{12}-\dfrac{7}{12}+\dfrac{22}{12}=\dfrac{75}{12}=\dfrac{25}{4}\)
\(C=\dfrac{-3}{4}\cdot8+\dfrac{1}{3}\cdot\dfrac{7}{2}-\dfrac{5}{18}=-6+\dfrac{7}{6}-\dfrac{5}{18}=\dfrac{-108}{18}+\dfrac{21}{18}-\dfrac{5}{18}=\dfrac{-92}{18}=\dfrac{-46}{9}\)

2: =1/2+1/2+1/2+1/2+1/2+1/2=6/2=3
3: \(=\dfrac{1\cdot3\cdot5\left(1+2+4+7\right)}{1\cdot5\cdot7\left(1+2+4+7\right)}=\dfrac{3}{7}\)

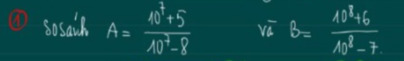
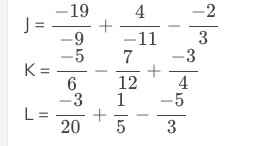
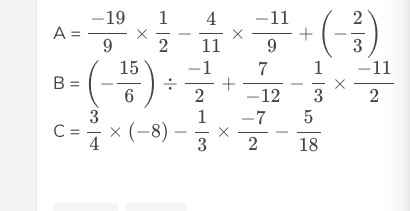 Trình bày chi tiết nhé
Trình bày chi tiết nhé
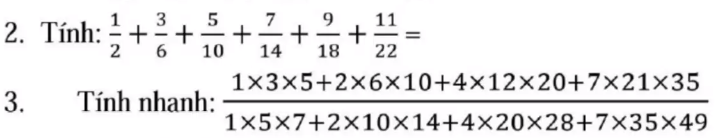



a) \(A=5x^2-2x+1=5\left(x^2-\dfrac{2}{5}x+\dfrac{1}{25}\right)+\dfrac{4}{5}\)
\(=5\left(x-\dfrac{1}{5}\right)^2+\dfrac{4}{5}\ge\dfrac{4}{5}\)
\(minA=\dfrac{4}{5}\Leftrightarrow x=\dfrac{1}{5}\)
b) \(B=2x^2+4y^2+12x-4y-5=2\left(x^2-6x+9\right)+\left(4y^2-4y+1\right)-15\)
\(=2\left(x-3\right)^2+\left(2y-1\right)^2-15\ge-15\)
\(minB=-15\Leftrightarrow\) \(\left\{{}\begin{matrix}x=3\\y=\dfrac{1}{2}\end{matrix}\right.\)
c) \(C=9x^2+3y^2+6xy-4y=\left(9x^2+6xy+y^2\right)+2\left(y^2-2y+1\right)-2\)
\(=\left(3x+y\right)^2+2\left(y-1\right)^2-2\ge-2\)
\(minC=-2\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=1\end{matrix}\right.\)