một vật dao động điều hòa có phương trình x=10cos(ωt +π/3)cm.trong một chu kỳ dao động, khoảng thời gian mà tốc độ của vật v >căn3.vmax/2 là 0.5 sẽ. tìm khoảng thời gian ngắn kể từ khi vật dao động đến khi vật qua vị trí có độ lớn gia tốc cực đại??
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 8 2016
mình nghĩ là vật đi qua 3 lân tức vật đã đi \(t=T+t1\)
tại \(t=0\) vật tại \(x=5\sqrt{3}\)
\(v>0\)
\Rightarrow \(s=4A+17-5\sqrt{3}\)
sử dung công thức
\(s=2A.\sin\left(\frac{\omega.t1}{2}\right)\)
\Rightarrow t1 = ?
vậy khoảng thời gian nhỏ nhất là \(t=T+t1\)
tại \(t=0\) vật tại \(x=5\sqrt{3}\)
\(v>0\)
\Rightarrow \(s=4A+17-5\sqrt{3}\)
sử dung công thức
\(s=2A.\sin\left(\frac{\omega.t1}{2}\right)\)
\Rightarrow t1 = ?
vậy khoảng thời gian nhỏ nhất là \(t=T+t1\)
TT
1 tháng 8 2016
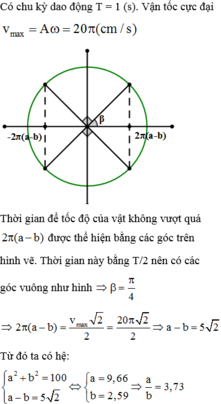
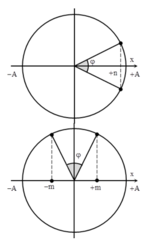
Trong một chu kỳ khoảng thời gian \(\left|v\right|\) <\(\frac{\sqrt{3}vmax}{2}\) => x=+ hoặc - A/2 vẽ lên hình ta thấy có 4 khoảng để thỏa mãn là từ A/2 đến biên (2 khoảng) và từ -A/2 đến biên (2 khoảng). Ta gọi mỗi đoạn là t.
Vậy ta có 0,4s= 4t =>t=0,1s=T/6 ( từ A/2 đến biên) nên T=0,6s.
Lúc t=0 thì vật ở vị trí x0 =5/2=A/2, v0 <0
Ở vị trí \(\left|a\right|\) =\(\frac{amax}{2}\) => x=+ hoặc trừ - A/2. Nhưng vì là khoẳng thời gian ngắn nên ta chọn -A/2 (A/2 đi theo chiều âm đến -A/2)
Vậy khoảng thời gian đó là \(\frac{T}{12}\) +\(\frac{T}{12}\) = 0,1S
VT
30 tháng 8 2019
Chọn D
+ Chu kỳ dao động: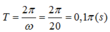 
+ Thời gian :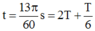 
+ Do t = 0 => x = A/2, v < 0, trong thời gian T = T/6 = T/12+T/12, vật đi từ A/2 đến –A/2 và trong thời gian 2T vật đi được quãng đường 8A.
Vậy tổng quãng đường vật đi trong thời gian trên là 8A+ A= 9A= 54cm.
VT
28 tháng 10 2018
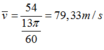
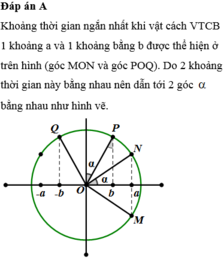
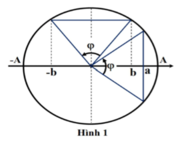
C ó sin α = b A cos α = a A ⇒ sin 2 α + cos 2 α = 1 ⇔ b 2 A 2 + a 2 A 2 = 1 ⇔ a 2 + b 2 = 100
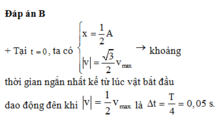
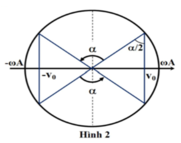
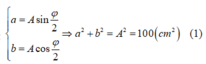
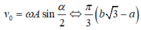
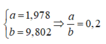
\(\left|v\right|>\frac{\sqrt{3}}{2}v_{max}\Rightarrow\left[{}\begin{matrix}v>\frac{\sqrt{3}}{2}v_{max}\\v< -\frac{\sqrt{3}}{2}v_{max}\end{matrix}\right.\)
\(\Delta t=\frac{0,5}{4}=\frac{1}{8}\left(s\right)\) ;\(\Delta t=\frac{1}{\omega}arc\cos\left(\frac{\sqrt{3}}{2}\right)\Rightarrow\omega=\frac{4}{3}\pi\left(rad/s\right)\)
\(a_{max}=\omega^2A=\frac{160}{9}\pi^2\left(cm/s^2\right)\)
Tại thời điểm t=0, gia tốc của vật là: \(a=-\omega^2A\cos\frac{\pi}{3}=-\frac{160}{9}\pi^2.\frac{1}{2}\left(cm/s^2\right)\)
\(\Rightarrow a=-\frac{1}{2}a_{max}\)
\(\Rightarrow\Delta t_1=\frac{1}{\omega}arc\sin\left(\frac{1}{2}\right)=\frac{3}{4\pi}.\frac{\pi}{6}=\frac{1}{8}\left(s\right)\)
\(\Delta t_2=\frac{T}{4}=\frac{3}{2.4}=\frac{3}{8}\left(s\right)\)
\(\Rightarrow\Delta t=t_1+t_2=....\)
P/s: Check lại số má giùm em nha :)
Sao suy ra denta t =0.5:4=1/8 vậy ạ