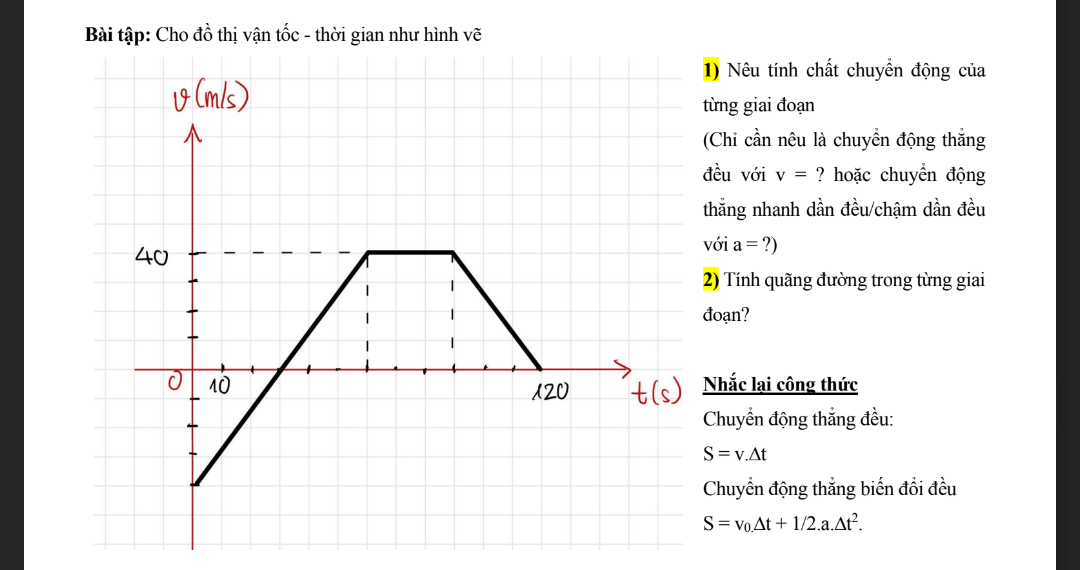
Mn giúp mình câu 17 với ạ, mai mình phải thi rồi.
Cảm ơn mn trước nha!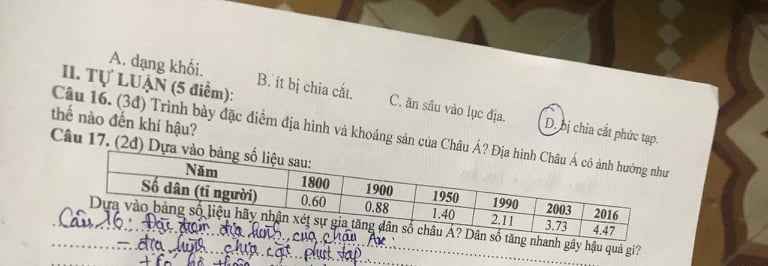
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
0
Những câu hỏi liên quan
HT
0
A
0
A
1
10 tháng 11 2021
\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)
A
1
8 tháng 11 2021
8.
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đt luôn đi qua với mọi m
\(\Leftrightarrow mx_0+2y_0-3my_0+m-1=0\\ \Leftrightarrow m\left(x_0-3y_0+1\right)+\left(2y_0-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-3y_0+1=0\\2y_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{2}\\y_0=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Vậy đt luôn đi qua \(A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) với mọi m
9.
PT giao Ox là \(y=0\Leftrightarrow mx+m-1=0\Leftrightarrow x=\dfrac{1-m}{m}\Leftrightarrow A\left(\dfrac{1-m}{m};0\right)\Leftrightarrow OA=\left|\dfrac{1-m}{m}\right|\)
PT giao Oy là \(x=0\Leftrightarrow\left(2-3m\right)y+m-1=0\Leftrightarrow y=\dfrac{1-m}{2-3m}\Leftrightarrow B\left(0;\dfrac{1-m}{2-3m}\right)\Leftrightarrow OB=\left|\dfrac{1-m}{2-3m}\right|\)
Để \(\Delta OAB\) cân thì \(OA=OB\Leftrightarrow\left|\dfrac{1-m}{m}\right|=\left|\dfrac{1-m}{2-3m}\right|\)
\(\Leftrightarrow\left|m\right|=\left|2-3m\right|\Leftrightarrow\left[{}\begin{matrix}m=2-3m\\m=3m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\) thỏa mãn đề
CL
0