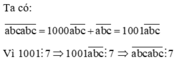Chứng minh: abcabc chia hết cho 11,13,7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
LA
1
KK
22 tháng 12 2015
1) abcd = ab x 100 + cd
= ab x 99 + ab + cd
Vậy nếu ab + cd chia hết cho 11
Thì abcd chia hết cho 11
CM
27 tháng 1 2019
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích số. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: a b c a b c ¯ = 1000 a b c ¯ + a b c ¯ = 1001 a b c ¯ Vì 1001 ⋮ 7 ⇒ 1001 a b c ¯ ⋮ 7 ⇒ a b c a b c ¯ ⋮ 7 |
NT
0
NH
3 tháng 7 2016
abcabc =abc x1001=abc x 7x143 chia hết cho 7
Vậy abcabc chia hết cho 7
3 tháng 7 2016
abcabc=1001*abc mà 1001 chia hết cho 7 nên abcabc chia hết cho 7
26 tháng 11 2015
Ta có:abcabc=abcx1001
Mà 1001=7x11x13
=>abcabc chia hết cho 7,11 ,13
LQ
31 tháng 7 2015
abcabc = abc x 1001 = abc x (7 x 11 x 13)
Suy ra: abcabc chia hết cho 7, cho 11 và cho 13