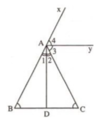
Cho tam giác ABC có góc B = góc C . Tia phân giác BAC cắt BC tại D . Qua điểm A vẽ tia Ay trong nằm trong nửa mặt phẳng bờ AB có chứa điểm C sao cho Ay song song với BC . Chứng minh Ay vuông góc với AD.
Bạn nào bt cách tick câu trả lời thì bảo mình luôn nhé.Mình chưa bt cách tick.=))

Vì \(\widehat{B}=\widehat{C}\Rightarrow\Delta ABC\text{ cân tại A }\Rightarrow AB=AC\)
Xét \(\Delta ABD\text{ và }\Delta ADC\) có :
\(\hept{\begin{cases}AB=AC\\\widehat{A_1}=\widehat{A_2}\\AD\text{ chung }\end{cases}\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)}\)
=> \(\widehat{D_1}=\widehat{D_2}\text{ mà }\widehat{D_1}+\widehat{D_2}=180^{\text{o}}\Rightarrow\widehat{D_1}=\widehat{D_2}=90^{\text{o}}\)
Mà Ay//BC
=> \(\widehat{A_{23}}+\widehat{D_2}=180^{\text{o}}\text{ mà }\widehat{D_2}=90^{\text{o}}\Rightarrow\widehat{A_{23}}=90^{\text{o}}\Rightarrow AD\perp Ay\left(\text{đpcm}\right)\)