C/m rằng với mọi giá trị của biến x ta luôn có:
a. -x2 + 4x - 5 < 0
b. x4 + 3x2 + 3 > 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HL
2
NC
26 tháng 8 2020
Bài làm:
a) Ta có: \(-x^2+4x-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1\le-1< 0\left(\forall x\right)\)
=> đpcm
b) \(x^4+3x^2+3=\left(x^4+3x^2+\frac{9}{4}\right)+\frac{3}{4}=\left(x^2+\frac{3}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\left(\forall x\right)\)
=> đpcm
26 tháng 8 2020
a) -x2 + 4x - 5 = -x2 + 4x - 4 - 1
= -( x2 - 4x + 4 ) - 1
= -( x - 2 )2 - 1 ≤ -1 < 0 ∀ x ( đpcm )
b) x4 + 3x2 + 3 ( * )
Đặt t = x2
(*) <=> t2 + 3t + 3
<=> ( t2 + 3t + 9/4 ) + 3/4
<=> ( t + 3/2 )2 + 3/4
<=> ( x2 + 3/2 )2 + 3/4 ≥ 3/4 > 0 ∀ x ( đpcm )
12 tháng 4 2018
Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~
13 tháng 8 2018
ms nghĩ câu b) đợi tí :)
b)
Ta có : x^4 luôn lớn hơn hoặc bằng 0
3x^2 luôn lớn hơn hoặc bằng 0
=> x^4 + 3x^2 luôn lớn hơn hoặc bằng 0
=> x^4 + 3x^2 + 3 luôn lớn hơn hoặc bằng 3 ( đpcm )
13 tháng 8 2018
a) Ta có: \(-x^2+4x-5=-\left(x^2-4x+5\right)=-\left(x-4\right)^2-1\)
Vì \(\left(x-4\right)^2\ge0\left(\forall x\right)\Rightarrow-\left(x-4\right)^2\le0\left(\forall x\right)\)
Và -1 < 0
Nên \(-x^2+4x-5< 0\left(\forall x\right)\)
b) \(x^4+3x^2+3=\left(x^4+2.x^2.\frac{3}{2}+\frac{9}{4}\right)+\frac{3}{4}=\left(x^2+\frac{3}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x^2+\frac{3}{2}\right)^2\ge0\left(\forall x\right)\)
Và \(\frac{3}{4}>0\)
Vậy...
c) \(x^2+2x+7=x^2+2x+1+6=\left(x+1\right)^2+6>6>0\) \(\left(\forall x\right)\)
Vậy ...
CM
10 tháng 7 2018
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
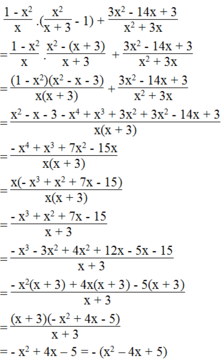
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
4 tháng 9 2021
a: Ta có: \(-x^2+4x-5\)
\(=-\left(x^2-4x+5\right)\)
\(=-\left(x^2-4x+4+1\right)\)
\(=-\left(x-2\right)^2-1< 0\forall x\)
4 tháng 9 2021
b: Ta có: \(x^4\ge0\forall x\)
\(3x^2\ge0\forall x\)
Do đó: \(x^4+3x^2\ge0\forall x\)
\(\Leftrightarrow x^4+3x^2+3>0\forall x\)
c: Ta có: \(\left(x^2+2x+3\right)=\left(x+1\right)^2+2>0\forall x\)
\(x^2+2x+4=\left(x+1\right)^2+3>0\forall x\)
Do đó: \(\left(x^2+2x+3\right)\left(x^2+2x+4\right)>0\forall x\)
\(\Leftrightarrow\left(x^2+2x+3\right)\left(x^2+2x+4\right)+3>0\forall x\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
Đặt \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(1\right)=-2< 0\)
\(f\left(2\right)=13>0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc khoảng (1;2)
\(f\left(-2\right)=13>0\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc khoảng (-2;1)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm phân biệt
a) Ta có: \(-x^2+4x-5\)
\(=-\left(x^2-4x+5\right)\)
\(=-\left(x^2-4x+4+1\right)\)
\(=-\left(x-2\right)^2-1\)
Ta có: \(\left(x-2\right)^2\ge0\forall x\)
\(\Leftrightarrow-\left(x-2\right)^2\le0\forall x\)
\(\Leftrightarrow-\left(x-2\right)^2-1\le-1< 0\forall x\)
hay \(-x^2+4x-5< 0\forall x\)(đpcm)
b) Ta có: \(x^4\ge0\forall x\)
\(3x^2\ge0\forall x\)
Do đó: \(x^4+3x^2\ge0\forall x\)
\(\Leftrightarrow x^4+3x^2+3\ge3>0\forall x\)
hay \(x^4+3x^2+3>0\forall x\)(đpcm)