Cho các số thực x,y với \(x\ge0\) thỏa mãn \(5^{x+3y}+5^{xy+1}+x\left(y+1\right)+1=5^{-xy-1}+\frac{1}{5^{x+3y}}-3y\) . Gọi m là giá trị nhỏ nhất của biểu thức T=x =2y +1. Tìm m?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
2 tháng 1 2021
Mình nghĩ phần phân thức là $3x+3y+2z$ thay vì $3x+3y+3z$. Nếu là vậy thì bạn tham khảo lời giải tại link sau:
Cho x, y, z là các số thực dương thỏa mãn đẳng thức xy yz zx=5. Tìm GTNN của biểu thức \(P=\frac{3x 3y 2z}{\sqrt{6\left(... - Hoc24
MT
2 tháng 1 2021
mình cảm ơn bạn nhiều ạ <3 bạn có thể giúp mình mấy câu mình vừa đăng không
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9 2021
Đặt \(\left\{{}\begin{matrix}\sqrt{2x+3}=a\ge0\\\sqrt{y}=b\ge0\end{matrix}\right.\)
\(\Rightarrow b\left(b^2+1\right)-3a^2=\left(a^2+1\right)a-3b^2\)
\(\Rightarrow a^3-b^3+3a^2-3b^2+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+\left(a-b\right)\left(3a+3b\right)+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2+3a+3b+1\right)=0\)
\(\Leftrightarrow a=b\Rightarrow\sqrt{2x+3}=\sqrt{y}\)
\(\Rightarrow y=2x+3\)
\(\Rightarrow M=x\left(2x+3\right)+3\left(2x+3\right)-4x^2-3\) tới đây chắc chỉ cần bấm máy
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2021
Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\)
\(\Leftrightarrow x^2+2\le3x\)
Hoàn toàn tương tự ta có \(y^2+2\le3y\)
Do đó: \(P\ge\dfrac{x+2y}{3x+3y+3}+\dfrac{2x+y}{3x+3y+3}+\dfrac{1}{4\left(x+y-1\right)}\)
\(P\ge\dfrac{x+y}{x+y+1}+\dfrac{1}{4\left(x+y-1\right)}\)
Đặt \(a=x+y-1\Rightarrow1\le a\le3\)
\(\Rightarrow P\ge f\left(a\right)=\dfrac{a+1}{a+2}+\dfrac{1}{4a}\)
\(f'\left(a\right)=\dfrac{3a^2-4a-4}{4a^2\left(a+2\right)^2}=\dfrac{\left(a-2\right)\left(3a+2\right)}{4a^2\left(a+2\right)^2}=0\Rightarrow a=2\)
\(f\left(1\right)=\dfrac{11}{12}\) ; \(f\left(2\right)=\dfrac{7}{8}\) ; \(f\left(3\right)=\dfrac{53}{60}\)
\(\Rightarrow f\left(a\right)\ge\dfrac{7}{8}\Rightarrow P_{min}=\dfrac{7}{8}\) khi \(\left(x;y\right)=\left(1;2\right);\left(2;1\right)\)
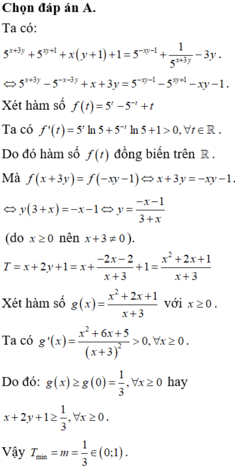
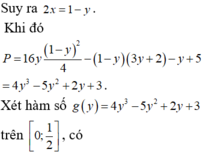
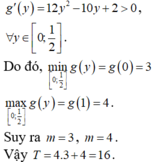
\(5^{x+3y}+5^{xy+1}+xy+1+x+3y=\frac{1}{5^{xy+1}}+\frac{1}{5^{x+3y}}\)
\(\Leftrightarrow5^{x+3y}-5^{-x-3y}+x+3y=5^{-xy-1}-5^{-\left(-xy-1\right)}+\left(-xy-1\right)\)
Xét hàm \(f\left(t\right)=5^t-\frac{1}{5^t}+t\Rightarrow f'\left(t\right)=5^t.ln5+\frac{ln5}{5^t}+1>0\)
\(\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow x+3y=-xy-1\)
\(\Rightarrow y\left(x+3\right)=-x-1\)
\(\Rightarrow y=\frac{-x-1}{x+3}\)
\(\Rightarrow T=f\left(x\right)=x-\frac{2x+2}{x+3}+1\)
\(f'\left(x\right)=\frac{\left(x+1\right)\left(x+5\right)}{\left(x+3\right)^2}>0;\forall x\ge0\)
\(\Rightarrow f\left(x\right)_{min}=f\left(0\right)=\frac{1}{3}\Rightarrow m=\frac{1}{3}\)