cosx= -cos (x+\(\frac{\pi}{3}\))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
a) Với mọi \(x \in \mathbb{R}\) ta có \( - 1 \le cosx \le 1\)
Vậy phương trình \(cosx = - 3\;\) vô nghiệm.
\(\begin{array}{l}b)\,\;cosx = cos{15^o}\;\\ \Leftrightarrow \left[ \begin{array}{l}x = {15^o} + k{360^o},k \in \mathbb{Z}\\x = - {15^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = {15^o} + k{360^o}\) hoặc \(x = - {15^o} + k{360^o},k \in \mathbb{Z}\).
\(\begin{array}{l}c)\;\,cos(x + \frac{\pi }{{12}}) = cos\frac{{3\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{{12}} = \frac{{3\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\\x + \frac{\pi }{{12}} = - \frac{{3\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}\\x = - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = \frac{\pi }{6} + k2\pi ,\) hoặc \(x = - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2020
\(\left[{}\begin{matrix}x+\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\x+\frac{\pi}{6}=-\frac{\pi}{6}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
Phuong Tran
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2020
\(\Leftrightarrow2cos\left(x+\frac{\pi}{6}\right).cos\left(\frac{\pi}{6}\right)=\frac{3}{2}-4sin\frac{x}{2}.sin\left(\frac{x}{2}+\frac{\pi}{6}\right)\)
\(\Leftrightarrow\sqrt{3}cos\left(x+\frac{\pi}{6}\right)=\frac{3}{2}+2\left[cos\left(x+\frac{\pi}{6}\right)-cos\frac{\pi}{6}\right]\)
\(\Leftrightarrow\sqrt{3}cos\left(x+\frac{\pi}{6}\right)=\frac{3}{2}+2cos\left(x+\frac{\pi}{6}\right)-\sqrt{3}\)
\(\Leftrightarrow\left(\sqrt{3}-2\right)cos\left(x+\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\left(\sqrt{3}-2\right)\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}=cos\left(\frac{\pi}{6}\right)\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2020
\(2sin\left(\frac{\pi}{2}+x\right)+sin\left(3\pi-x\right)+sin\left(\frac{3\pi}{2}+x\right)+cos\left(\frac{\pi}{2}+x\right)\)
\(=2cosx+sinx-cosx-sinx\)
\(=cosx\)
21 tháng 8 2023
a: cosx=3
mà -1<=cosx<=1
nên \(x\in\varnothing\)
b: \(cosx=\dfrac{\sqrt{3}}{2}\)
=>\(cosx=cos\left(\dfrac{pi}{6}\right)\)
=>x=pi/6+k2pi hoặc x=-pi/6+k2pi
c: \(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{pi}{12}=\dfrac{3}{12}pi+k2pi\\x+\dfrac{pi}{12}=-\dfrac{3}{12}pi+k2pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{12}pi+k2pi=\dfrac{1}{6}pi+k2pi\\x=-\dfrac{4}{12}pi+k2pi=-\dfrac{1}{3}pi+k2pi\end{matrix}\right.\)
d: =>x-20 độ=70 độ+k*360 hoặc x-20=-70+k*360
=>x=90+k*360 hoặc x=-50+k*360
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2019
\(cosx+cos\left(x+\frac{\pi}{5}\right)+cos\left(x+\frac{9\pi}{5}\right)+cos\left(x+\frac{2\pi}{5}\right)+cos\left(x+\frac{8\pi}{5}\right)+...+cos\left(x+\frac{5\pi}{5}\right)\)
\(=cosx-2cosx.cos\frac{4\pi}{5}-2cosx.cos\frac{3\pi}{5}-2cosx.cos\frac{2\pi}{5}-2cosx.cos\frac{\pi}{5}-cosx\)
\(=-2cosx\left(cos\frac{\pi}{5}+cos\frac{4\pi}{5}+cos\frac{2\pi}{5}+cos\frac{3\pi}{5}\right)\)
\(=-2cosx\left(2cos\frac{\pi}{2}.cos\frac{3\pi}{10}+2cos\frac{\pi}{2}cos\frac{\pi}{10}\right)\)
\(=0\) (do \(cos\frac{\pi}{2}=0\))
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2020
c/
ĐKXĐ: ...
Đặt \(cosx+\frac{2}{cosx}=a\Rightarrow cos^2x+\frac{4}{cos^2x}=a^2-4\)
Pt trở thành:
\(9a+2\left(a^2-4\right)=1\)
\(\Leftrightarrow2a^2+9a-9=0\)
Pt này nghiệm xấu quá bạn :(
d/ĐKXĐ: ...
Đặt \(\frac{2}{cosx}-cosx=a\Rightarrow cos^2x+\frac{4}{cos^2x}=a^2+4\)
Pt trở thành:
\(2\left(a^2+4\right)+9a-1=0\)
\(\Leftrightarrow2a^2+9a+7=0\Rightarrow\left[{}\begin{matrix}a=-1\\a=-\frac{7}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\frac{2}{cosx}-cosx=-1\\\frac{2}{cosx}-cosx=-\frac{7}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-cos^2x+cosx+2=0\\-cos^2x+\frac{7}{2}cosx+2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}cosx=-1\\cosx=2\left(l\right)\\cosx=4\left(l\right)\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2020
b/
ĐKXĐ: ...
Đặt \(sinx+\frac{1}{sinx}=a\Rightarrow sin^2x+\frac{1}{sin^2x}=a^2-2\)
Pt trở thành:
\(4\left(a^2-2\right)+4a=7\)
\(\Leftrightarrow4a^2+4a-15=0\Rightarrow\left[{}\begin{matrix}a=\frac{3}{2}\\a=-\frac{5}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sinx+\frac{1}{sinx}=\frac{3}{2}\\sinx+\frac{1}{sinx}=-\frac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin^2x-\frac{3}{2}sinx+1=0\left(vn\right)\\sin^2x+\frac{5}{2}sinx+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-\frac{1}{2}\\sinx=-2\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
DN
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 9 2020
\(y=2cos\left(x+\frac{\pi}{6}\right)cos\left(\frac{\pi}{6}\right)=\sqrt{3}cos\left(x+\frac{\pi}{6}\right)\)
Do \(-1\le cos\left(x+\frac{\pi}{6}\right)\le1\) nên \(-\sqrt{3}\le y\le\sqrt{3}\)
\(y_{min}=-\sqrt{3}\) khi \(cos\left(x+\frac{\pi}{6}\right)=-1\)
\(y_{max}=\sqrt{3}\) khi \(cos\left(x+\frac{\pi}{6}\right)=1\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vẽ đồ thị:
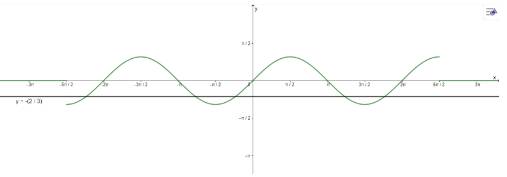
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 9 2020
3.
a.
\(\Leftrightarrow\left(cos3x-cosx\right)+\left(cos2x-1\right)=0\)
\(\Leftrightarrow-2sin2x.sinx+1-2sin^2x-1=0\)
\(\Leftrightarrow sin2x.sinx+sin^2x=0\)
\(\Leftrightarrow2sin^2x.cosx+sin^2x=0\)
\(\Leftrightarrow sin^2x\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow cosx=cos\left(\pi-x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow cosx=cos\left(\frac{2\pi}{3}-x\right)\)
\(\Leftrightarrow x=\frac{2\pi}{3}-x+k2\pi\)
\(\Leftrightarrow x=\frac{\pi}{3}+k2\pi\)