Cho sin2α = a. Tính cos4α - sin4α
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
1
25 tháng 6 2023
Ta có:
`sin^4 \alpha + cos^4 \alpha -sin^6 \alpha- cos^6\alpha`
`=sin^4\alpha+cos^4\alpha-(sin^2\alpha+cos^2\alpha)(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha)`
`=sin^4\alpha + cos^4\alpha-(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha)`
`=sin^2\alpha cos^2\alpha(ĐPCM)`
25 tháng 7 2023
a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)
25 tháng 6 2023
a: \(VT=\dfrac{\left(sina+cosa\right)^3-3\cdot sina\cdot cosa\left(sina+cosa\right)}{sina+cosa}\)
=(sina+cosa)^2-3*sina*cosa
=sin^2a+cos^2a-sina*cosa
=1-sina*cosa=VP
c: VT=(sin^2a+cos^2a)^2-2*sin^2a*cos^2a-(sin^2a+cos^2a)^3+3*sin^2a*cos^2a*(sin^2a+cos^2a)
=1-2sin^2a*cos^2a-1+3*sin^2a*cos^2a
=sin^2a*cos^2a=VP
MB
1
24 tháng 8 2023
\(A=sin^4a+2\cdot sin^4a\cdot cos^2a+cos^4a+2\cdot cos^4a\cdot sin^2a\)
\(=\left(sin^4a+cos^4a\right)+2\cdot sina^2a\cdot cos^2a\left(sin^2a+cos^2a\right)\)
\(=sin^4a+cos^4a+2\cdot sin^2a\cdot cos^2a\)
\(=\left(sin^2a+cos^2a\right)^2=1\)
PT
1
CM
2 tháng 11 2017
Ta có (sinα + cosα ) 2 = sin 2 α + 2sinαcosα + cos 2 α = 1 + 2sinαcosα
Mặt khác sinα + cosα = m nên sinα + cosα = m ⇔ (sinα + cosα ) 2 = m 2
⇔ sin 2 α + cos 2 α + 2sinαcosα = m 2
⇔ 1 + 2sinαcosα = m 2
⇔ 2sinαcosα = m 2 - 1
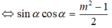
Đặt A = |sin4 α - cos 4 α |.
Ta có:
A = | sin 4 α - cos4α |
= |( sin 2 α - cos 2 α )( sin 2 α + cos 2 α )|
=|(sinα + cosα )(sinα - cosα )|
⇒ A 2 = (sinα + cosα ) 2 (sinα - cosα ) 2 = (1 + 2sinxcosx)(1 - 2sinxcosx)
⇒ A 2 = (1 + 2sinxcosx)(1 - 2sinxcosx )
CH
17 tháng 8 2021
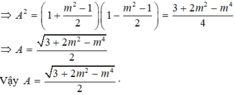
\(\left(sin^2\alpha\right)^2+\left(cos^2\alpha\right)^2+2.sin\alpha.cos\alpha\\ =\left(sin^2\alpha+cos^2\alpha\right)^2\\ =\left(1\right)^2=1\)
29 tháng 7 2023
cos^4a-sin^4a
=(cos^2a-sin^2a)(cos^2a+sin^2a)
=cos^2a-sin^2a
=cos2a
CM
18 tháng 7 2017
A = 4 [ ( sin 2 α + cos 2 α ) 2 - 2 sin 2 α cos 2 α ] - cos4α
= 4 ( 1 - sin 2 2 α / 2 ) - 1 + 2 sin 2 2 α = 3
\(cos^4\alpha-sin^4\alpha=\left(cos^2\alpha-sin^2\alpha\right)\left(cos^2\alpha+cos^2a\right)\)
\(=cos^2\alpha-sin^2\alpha=\left(1-sin^2\alpha\right)-sin^2\alpha\)
\(=1-2sin^2\alpha=1-2a\)