27. Trên khoảng ( π/2;π) pt cos ( π/6 - 2x) = sinx có bao nhiêu nghiệm?
19. Vs những giá trị nào của x thì giá trị của các hàm số y = sin3x và y =sinx bằng nhau?
33. Giải pt : tan3x.cot2x =1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)

- Hàm số y = cosx trên đoạn [(-π)/2; 3π/2]:
Các khoảng tăng: [(-π)/2,0], [π, 3π/2].
Các khoảng giảm: [0, π ],.
- Hàm số y = |x| trên khoảng (-∞; +∞)
Khoảng tăng: [0, +∞)
Khoảng giảm (-∞, 0].

Đáp án: D.
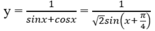
Trên khoảng (0; π/2), sin(x + π/4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π/4
Suy ra giá trị nhỏ nhất của hàm số là min y = y(π/4) = 2 /2.

Đáp án C
Điểm M thuộc xx’ dao động với biên độ cực đại khi
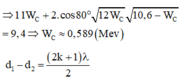
Do M là điểm cực đại gần C nhất nên M nằm trên đường cực đại thứ nhất : k = 0
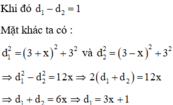
Dựa vào đáp án ta chọn đáp án C thõa mãn do nếu xét riêng trên CD khi M gần C nhất thì AM ngắn nhất
27.
\(\cos\left(\frac{\pi}{6}-2x\right)=\sin x\)
\(\Leftrightarrow\sin\left(\frac{\pi}{2}-\frac{\pi}{6}+2x\right)=\sin x\)
\(\Leftrightarrow\sin\left(\frac{\pi}{3}+2x\right)=\sin x\)
\(\Leftrightarrow\frac{\pi}{3}+2x=\pi-x+k2\pi\Leftrightarrow x=\frac{2}{9}\pi+\frac{2}{3}k\pi\)
\(\frac{\pi}{2}< \frac{2}{9}\pi+\frac{2}{3}k\pi< \pi\Leftrightarrow\frac{5}{18}\pi< \frac{2}{3}k\pi< \frac{7}{9}\pi\)
\(\Leftrightarrow\frac{5}{12}< k< \frac{7}{6}\Rightarrow k=1\)
Vậy phương trình có 1 nghiệm thuộc khoảng \(\left(\frac{\pi}{2};\pi\right)\)
19. \(\sin3x=\sin x\Leftrightarrow3x=\pi-x+k2\pi\Rightarrow x=\frac{\pi}{4}+\frac{1}{2}k\pi\)
33. \(DKXD:\left\{{}\begin{matrix}\cos3x\ne0\\\sin2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x\ne\frac{\pi}{2}+k\pi\\2x\ne\pi+k\pi\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{6}+\frac{1}{3}k\pi\\x\ne\frac{\pi}{2}+\frac{1}{2}k\pi\end{matrix}\right.\)
\(\tan3x.\cot2x=1\Leftrightarrow\tan3x=\frac{1}{\cot2x}=\tan2x\)
\(\Leftrightarrow3x=\pi+2x+k\pi\Leftrightarrow x=\pi+k\pi\) (t/m)