tích phân \(\frac{dx}{\sqrt{1-cosx}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\int \frac{x}{\sqrt{x+2}}dx \\ = \int \frac{x+2-2}{\sqrt{x+2}}dx \\ = \int \sqrt{x+2}-2\frac{1}{\sqrt{x+2}}dx \\ = \frac{2}{3}(x+2)^{\frac{3}{2}}-4\sqrt{x+2}+C\)
\(B=\int \frac{sinx+cosx}{\sqrt[3]{1-sin2x}}dx \\ x=\frac{\pi}{4}-u, dx=-du \\ =- \int \frac{sin(\frac{\pi}{4}-u)+cos(\frac{\pi}{4}-u)}{\sqrt[3]{1-sin(\frac{\pi}{2}-2u)}}du \\ = - \int \frac{\frac{1}{\sqrt2}cosu+\frac{1}{\sqrt2}sinu+\frac{1}{\sqrt2}cosu-\frac{1}{\sqrt2}sinu}{\sqrt[3]{1-cos2u}}du \\ = -\int \frac{\frac{2}{\sqrt2}cosu}{\sqrt[3]{1-cos2u}}du \\ = -\sqrt2 \int \frac{cosu}{\sqrt[3]{1-cos^2u+sin^2u}}du \\ = -\sqrt2 \int \frac{cosu}{\sqrt[3]{2sin^2u}}du \\ v=sinu, dv=cosudu \\ = -\sqrt2 \int \frac{1}{\sqrt[3]{2v^2}}dv \\ = -\frac{\sqrt2}{\sqrt[3]2} \int v^{-\frac{2}{3}}dv \\ = -\frac{\sqrt2}{\sqrt[3]2} 3v^\frac{1}{3}+C \\ = -\frac{\sqrt2}{\sqrt[3]2} 3\sqrt[3]{sin(\frac{\pi}{4}-x)}+C \)

Đặt u = x và dv = cos(a - x)dx ,suy ra du = dx và v = -sin(a-x). Do đó
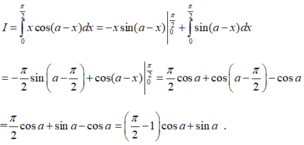
Vậy chọn đáp án C.

Lời giải:
\(\int ^{\frac{\pi}{2}}_{0}\frac{\sin 2x\cos x}{1+\cos x}dx=\int ^{\frac{\pi}{2}}_{0}\frac{2\sin x\cos ^2x}{\cos x+1}dx=2\int ^{\frac{\pi}{2}}_{0}\frac{\cos^2x\sin xdx}{\cos x+1}\)
\(=2\int ^{\frac{\pi}{2}}_{0}\frac{-\cos ^2xd(\cos x)}{\cos x+1}=2\int ^{0}_{1}\frac{-t^2dt}{t+1}=2\int ^{1}_{0}\frac{t^2}{t+1}dt\)
\(=2\int^1_0\frac{(t^2-1)+1}{t+1}dt=2\int ^1_0(t-1+\frac{1}{t+1})dt\)
\(=2(\frac{t^2}{2}-t+\ln|t+1|)|^{1}_0=2\ln 2-1\)

\(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{1}{sin^4x.cosx}d\pi x\)
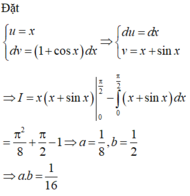

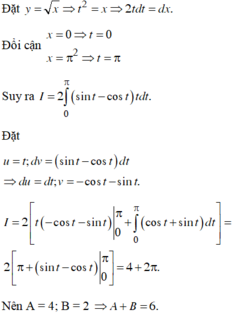
Tex bị lỗi. Mình viết tích phân bạn cố xem nhé!
I = tích phân \(\frac{dx}{\sqrt{1-cosx}}\)= tích phân \(\frac{\sqrt{1+\cos x}}{\sin x}dx\)
= tích phân \(\frac{\sqrt{1+\cos x}.\sin x}{\sin^2x}dx\)
Đặt: \(\sqrt{1+\cos x}=t\)
<=> \(1+\cos x=t^2\Leftrightarrow-2\sin xdx=2tdt\Leftrightarrow\sin xdx=-tdt\)
và \(\cos x=t^2-1\Leftrightarrow\cos^2x=\left(t^2-1\right)^2\Leftrightarrow1-\cos^2x=1-\left(t^2-1\right)^2\)
\(\Leftrightarrow\sin^2x=1-t^4+2t^2-1=-t^2\left(t^2-2\right)\)
=> I = tích phân \(\frac{-t^2dt}{-t^2\left(t^2-2\right)}\)= tích phân \(\frac{dt}{t^2-2}\)
= tích phân \(\frac{1}{2\sqrt{2}}\left(\frac{1}{t-\sqrt{2}}-\frac{1}{t+\sqrt{2}}\right)dx\)
Tự làm tiếp nhé!
còn có 1 cách khác: \(1-\cos x=2\sin^2\frac{s}{2}\)
\(\frac{1}{\sqrt{1-\cos x}}=\frac{1}{\sqrt{2\sin^2\frac{x}{2}}}=\frac{1}{\sqrt{2}\sin\frac{x}{2}}=\frac{1}{\sqrt{2}}\frac{\sin\frac{x}{2}}{1-\cos^2\frac{x}{2}}\)
Đặt: \(\cos\frac{x}{2}=t\Leftrightarrow\frac{1}{2}\sin\frac{x}{2}dx=dt\Leftrightarrow\sin\frac{x}{2}dx=2dt\)
I = tích phân \(\frac{\sqrt{2}dt}{1-t^2}\) làm tiếp