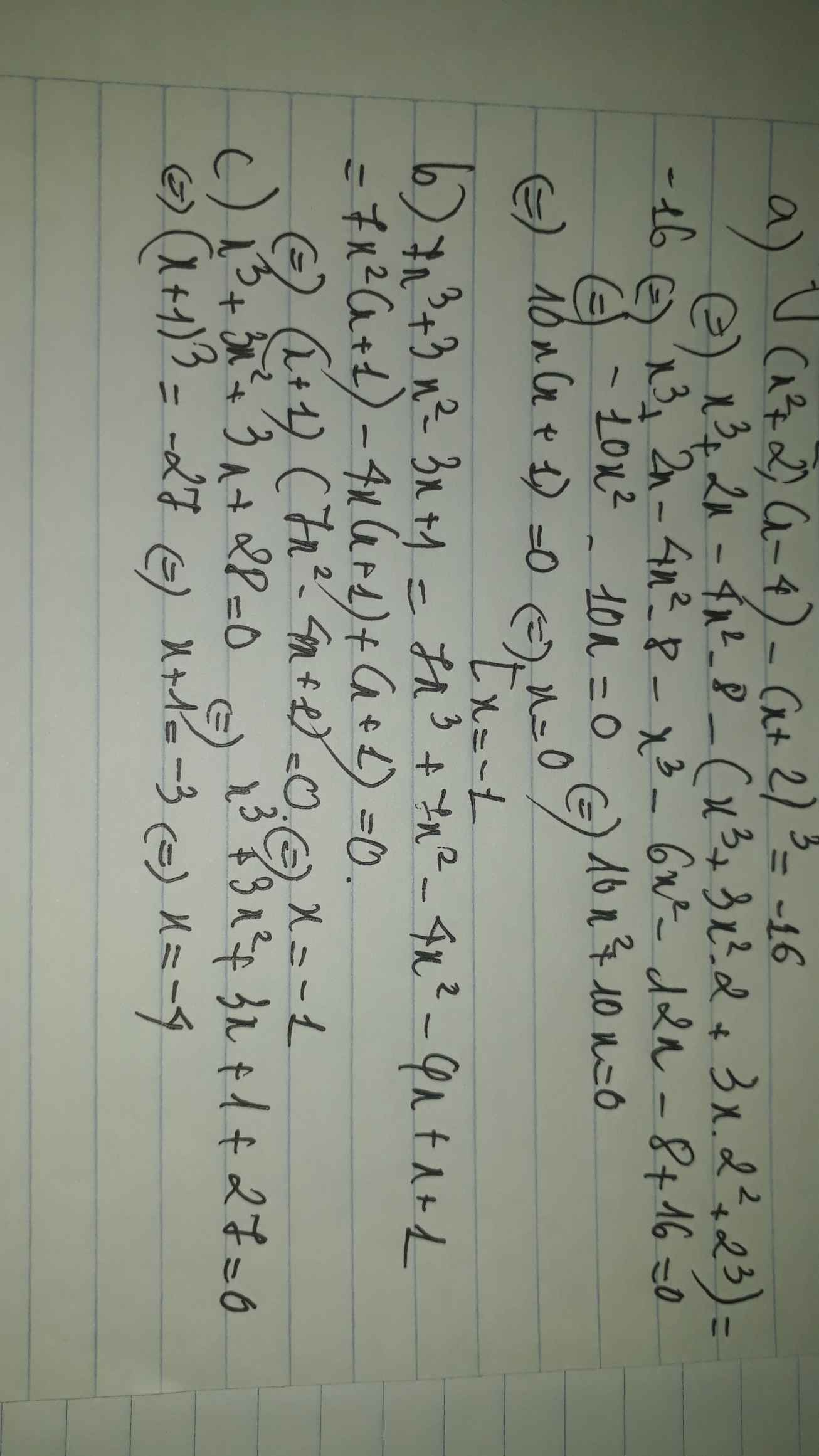3x2-4\(\sqrt{x}+4=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
2
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
ĐKXĐ: \(-\dfrac{4}{3}\le x\le5\)
\(\left(\sqrt{3x+4}-4\right)+\left(1-\sqrt{5-x}\right)+\left(3x^2-8x-16\right)=0\)
\(\Leftrightarrow\dfrac{3\left(x-4\right)}{\sqrt{3x+4}+4}+\dfrac{x-4}{1+\sqrt{5-x}}+\left(x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(\dfrac{3}{\sqrt{3x+4}+4}+\dfrac{1}{1+\sqrt{5-x}}+3x+4\right)=0\)
\(\Leftrightarrow x-4=0\)
\(\Leftrightarrow x=4\)
30 tháng 7 2021
\(\sqrt{3x+4}-\sqrt{5-x}+3x^2-8x-19=0\) (\(5\ge x\ge\dfrac{-4}{3}\))
Vì 2 vế không âm, theo BĐT Cô-si ta được:
\(\dfrac{3x+4+1}{2}\ge\sqrt{3x+4}\)
\(\dfrac{5-x+1}{2}\ge\sqrt{5-x}\) \(\Rightarrow\) \(\dfrac{x-6}{2}\le-\sqrt{5-x}\)
Dấu "=" xảy ra khi và chỉ khi \(\left[{}\begin{matrix}3x+4=1\\5-x=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=-1\left(KTM\right)\\x=4\left(TM\right)\end{matrix}\right.\)
Thay vào pt trên thấy pt luôn đúng nên x = 4 TMĐK
Vậy ...
Chúc bn học tốt! (Có gì sai mong bạn bỏ qua)
NV
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
\(y'=\left(3x^2+4\right)'\sqrt{x}+\left(3x^2+4\right).\left(\sqrt{x}\right)'=6x\sqrt{x}+\dfrac{3x^2+4}{2\sqrt{x}}=\dfrac{15x^2+4}{2\sqrt{x}}\)
14 tháng 8 2021
a: Ta có: \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)^3=-16\)
\(\Leftrightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)
\(\Leftrightarrow-10x^2-10x=0\)
\(\Leftrightarrow-10x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
c: Ta có: \(x^3+3x^2+3x+28=0\)
\(\Leftrightarrow\left(x+1\right)^3=-27\)
\(\Leftrightarrow x+1=-3\)
hay x=-4
26 tháng 11 2021
\(x^2=1\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(x^2=3\Rightarrow\left[{}\begin{matrix}x=-\sqrt{3}\\x=\sqrt{3}\end{matrix}\right.\)
\(x^2=5\Rightarrow\left[{}\begin{matrix}x=-\sqrt{5}\\x=\sqrt{5}\end{matrix}\right.\Rightarrow x=-\sqrt{5}\left(vì.x< 0\right)\)
\(x^2=7\Rightarrow\left[{}\begin{matrix}x=-\sqrt{7}\\x=\sqrt{7}\end{matrix}\right.\Rightarrow x=-\sqrt{7}\left(vì.x< 0\right)\)
\(x^2=9\Rightarrow\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
\(\left(x-2\right)^2=2\Rightarrow\left[{}\begin{matrix}x-2=-\sqrt{2}\\x-2=\sqrt{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{2}\\x=2+\sqrt{2}\end{matrix}\right.\)
\(\left(x-4\right)^2=4\Rightarrow\left[{}\begin{matrix}x-2=-2\\x-2=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(\left(x-6\right)^2=6\Rightarrow\left[{}\begin{matrix}x-6=-\sqrt{6}\\x-6=\sqrt{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6-\sqrt{6}\\x=6+\sqrt{6}\end{matrix}\right.\)
\(\left(x-8\right)^2=8\Rightarrow\left[{}\begin{matrix}x-8=-2\sqrt{2}\\x-8=2\sqrt{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=8-2\sqrt{2}\\x=2+2\sqrt{2}\end{matrix}\right.\)
\(\left(x-10\right)^2=10\Rightarrow\left[{}\begin{matrix}x-10=-\sqrt{10}\\x-10=\sqrt{10}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=10-\sqrt{10}\\x=10+\sqrt{10}\end{matrix}\right.\)
\(\left(x-\sqrt{3}\right)^2=3\Rightarrow\left[{}\begin{matrix}x-\sqrt{3}=-\sqrt{3}\\x-\sqrt{3}=\sqrt{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\sqrt{3}\end{matrix}\right.\)
\(\left(x-\sqrt{5}\right)^2=5\Rightarrow\left[{}\begin{matrix}x-\sqrt{5}=-\sqrt{5}\\x-\sqrt{5}=\sqrt{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\sqrt{5}\end{matrix}\right.\)
PT
1
CM
18 tháng 4 2018
-3x2 + x + 4 ≥ 0
Xét tam thức f(x) = -3x2 + x + 4 có hai nghiệm x = -1 và x = 4/3, hệ số a = -3 < 0.
Do đó f(x) ≥ 0 khi -1 ≤ x ≤ 4/3.
Vậy tập nghiệm của bất phương trình là: T = [-1; 4/3]
T
27 tháng 10 2023
a, Sửa đề:
\(3x^2-\sqrt3 x+\dfrac14(dkxd:x\geq0)\\=(x\sqrt3)^2-2\cdot x\sqrt3\cdot\dfrac12+\Bigg(\dfrac12\Bigg)^2\\=\Bigg(x\sqrt3-\dfrac12\Bigg)^2\)
b,
\(x^2-x-y^2+y\\=(x^2-y^2)-(x-y)\\=(x-y)(x+y)-(x-y)\\=(x-y)(x+y-1)\)
c,
\(x^4+x^3+2x^2+x+1\\=(x^4+x^3+x^2)+(x^2+x+1)\\=x^2(x^2+x+1)+(x^2+x+1)\\=(x^2+x+1)(x^2+1)\)
d,
\(x^3+2x^2+x-16xy^2\\=x(x^2+2x+1-16y^2)\\=x[(x+1)^2-(4y)^2]\\=x(x+1-4y)(x+1+4y)\\Toru\)
XO
12 tháng 2 2023
a) (*) m = 0 => x = \(\dfrac{7}{8}\) (loại)
(*) \(m\ne0\) Phương trình có nghiệm
\(\Delta=\left[2\left(m-4\right)\right]^2-4m\left(m+7\right)=-60m+64\ge0\Leftrightarrow m\le\dfrac{16}{15}\)
Hệ thức Viet kết hợp 4x1 + 3x2 = 1
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2=\dfrac{m+7}{m}\\x_1+x_2=\dfrac{8-2m}{m}\\x_1=2x_2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2=\dfrac{m+7}{m}\\x_1=\dfrac{16-4m}{3m}\\x_2=\dfrac{8-2m}{3m}\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{16-4m}{3m}.\dfrac{8-2m}{3m}=\dfrac{m+7}{m}\)
\(\Leftrightarrow2\left(8-2m\right)^2=9m\left(m+7\right)\)
\(\Leftrightarrow8m^2-64m+128=9m^2+63m\)
\(\Leftrightarrow m^2+127m-128=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=128\left(\text{loại}\right)\end{matrix}\right.\)<=> m = 1
2
10 tháng 5 2022
Có: `x-2y+4=0`
`<=>x=2y-4`
Thay `x=2y-4` vào `(E)` có:
`3(2y-4)^2+4y^2-48=0`
`<=>3(4y^2-16y+16)+4y^2-48=0`
`<=>12y^2-48y+48+4y^2-48=0`
`<=>` $\left[\begin{matrix} y=3\\ y=0\end{matrix}\right.$
`@y=3=>x=2.3-4=2`
`@y=0=>x=2.0-4=-4`
`=>` Tọa độ giao điểm của `(E)` và `(d)` là: `(2;3)` và `(-4;0)`
`->D`
10 tháng 5 2022
\(\Rightarrow\) \(chọn\) \(D\)
\(xét\) \(hpt\) \(:\)
\(\left\{{}\begin{matrix}3x^2+4y^2-48=0\\x-2y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(2y-4\right)^2+4y^2-48=0\\x=2y-4\end{matrix}\right.\)
\(giải:\) \(3\left(4y^2-16y+16\right)+4y^2-48=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}12y^2-48y+48+4y^2-48=0\\16y^2-48y=0\\\left[{}\begin{matrix}y=0\Rightarrow x=-4\\y=3\Rightarrow x=2\end{matrix}\right.\end{matrix}\right.\)
\(vậy\) \(giao\) \(điểm\) \(của\) \(elip\) \(\left(E\right)\) \(là\) \(\left(-4;0\right)\) \(và\) \(\left(2;3\right)\)