Hoàng có 18 tờ tiền loại mệnh giá 2000 đồng, 5000 đồng và 10 000 đồng. Biết rằng tổng số tiền loại 5000 đồng và 10 000 đồng là bằng nhau và tổng giá trị của 18 tờ tiền là 92 000 đồng. Hỏi Hoàng có bao nhiêu tờ tiền mỗi loại?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2022
Tham khảo!
Gọi x , y , z là tờ giấy bạc theo thứ tự là loại : 20000 đồng , 50000 đồng , 100000 đồng
Ta có x + y + z = 16 ; 20000x = 50000y = 100000z
⇒20000x100000=50000y100000=100000z100000=x5=y2=z1⇒20000x100000=50000y100000=100000z100000=x5=y2=z1
Theo t/c của dãy tỉ số bằng nhau ta có :
x5=y2=z1=x+y+z5+2+1=168=2x5=y2=z1=x+y+z5+2+1=168=2
x5=2⇒x=2.5=10x5=2⇒x=2.5=10
y2=2⇒y=2.2=4y2=2⇒y=2.2=4
z1=2⇒2.1=2z1=2⇒2.1=2
Vậy mỗi loại có số tờ theo thứ tự lần lượt là: 10 ; 4 ; 2
14 tháng 7 2021
Gọi số tờ tiền loại 2000đ là a, 5000đ là b, 10000đ là c => a + b + c =16
Ta có: a.2000 = b.5000 = c.10000
⇒a:12000=b:15000=c:110000⇒a:12000=b:15000=c:110000
⇒a12000=b15000=c110000⇒a12000=b15000=c110000
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a12000=b15000=c110000=a+b+c12000+15000+110000=1611250=20000a12000=b15000=c110000=a+b+c12000+15000+110000=1611250=20000
⇒a12000=20000⇒a=20000.12000=10⇒a12000=20000⇒a=20000.12000=10
b15000=20000⇒b=20000.15000=4b15000=20000⇒b=20000.15000=4
c110000=20000⇒c=20000.110000=2c110000=20000⇒c=20000.110000=2
Vậy ...
Chúc cậu hok tốt!
AH
Akai Haruma
Giáo viên
19 tháng 12 2021
Lời giải:
Gọi số tờ tiền mệnh giá 2000, 5000, 10000 lần lượt là $a,b,c$. Theo bài ra ta có:
$a+b+c=16$
$2000a=5000b=10000c$
$\Rightarrow \frac{a}{5}=\frac{b}{2}=\frac{c}{1}$ (chia mỗi vế cho $10000$)
Áp dụng TCDTSBN:
$\Rightarrow \frac{a}{5}=\frac{b}{2}=\frac{c}{1}=\frac{a+b+c}{5+2+1}=\frac{16}{8}=2$
$\Rightarrow a=5.2=10; b=2.2=4; c=2.1=2$
Tổng giá trị 3 loại tiền là:
$3.10000.2=60000$ (đồng)
TN
13 tháng 7 2017
Gọi a,b,c lần lượt là số tờ giấy bạc loại 2000đ,5000đ và 10000đ.(a,b,c \(\in N^{\cdot}\))
Theo đề bài,ta có \(2000a=5000b=10000c\) và \(a+b+c=16\)
\(\Rightarrow\dfrac{2000a}{10000}=\dfrac{5000b}{10000}=\dfrac{10000c}{10000}\) và \(a+b+c=16\)
\(\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{c}{1}\) và \(a+b+c=16\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{c}{1}=\dfrac{a+b+c}{5+2+1}=\dfrac{16}{8}=2\)
Với\(\dfrac{a}{5}=2\Rightarrow a=10\)
\(\dfrac{b}{2}=2\Rightarrow b=4\)
\(\dfrac{c}{1}=2\Rightarrow c=2\)
Vậy loại 2000đ mua được 10 tờ
loại 5000đ mua được 4 tờ
loại 10000đ mua được 2 tờ
DT
12 tháng 11 2018
Gọi a,b,c lần lượt là số tờ giấy bạc loại 2000đ,5000đ và 10000đ.(a,b,c ∈N⋅∈N⋅)
Theo đề bài,ta có 2000a=5000b=10000c2000a=5000b=10000c và a+b+c=16a+b+c=16⇒2000a10000=5000b10000=10000c10000⇒2000a10000=5000b10000=10000c10000 và a+b+c=16a+b+c=16
⇒a5=b2=c1⇒a5=b2=c1 và a+b+c=16a+b+c=16
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
a5=b2=c1=a+b+c5+2+1=168=2a5=b2=c1=a+b+c5+2+1=168=2
Với a5=2⇒a=10a5=2⇒a=10
b2=2⇒b=4b2=2⇒b=4
c1=2⇒c=2c1=2⇒c=2
Vậy loại 2000đ mua được 10 tờ
loại 5000đ mua được 4 tờ
loại 10000đ mua được 2 tờ
VK
22 tháng 4 2017
Gọi x là số tờ giấy bạc loại 5000 đồng.
Số tờ giấy bạc loại 2000 đồng là 15 - x (=> điều kiện 0 < x < 15; nguyên)
Vì số tiền không quá 70000 nên:
Vì x là số nguyên dương nên x có thể là số nguyên dương từ 1 đến 13. Hay x có thể nhận các giá trị là {1; 2; 3; ...; 13}
Vậy số tờ giấy bạc loại 5000 đồng người ấy có thể có là các số nguyên dương thỏa mãn 1 ≤ x ≤ 13.
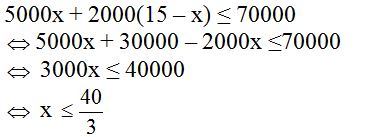
Gọi số tờ tiền loại 2000 đồng là a ; loại 5000 đồng là b ; loại 10 000 đồng là c
Ta có : a + b + c = 18 (1)
Lại có : 5000 x b = 10000 x c
=> b = 2 x c
Mặt khác 2000 x a + 5000 x b + 10000 x c = 92000
=> 2000 x a + 5000 x b + 5000 x b = 92000 (Vì 5000 x b = 10000 x c)
=> 2000 x a + 10000 x b = 92000
=> 2000 x (a + 5 x b) = 92000
=> a + 5 x b = 46(2)
Khi đó (1) <=> a + b + c =18
<=> a + b + c = 18
=> a + 3 x c = 18(3) (vì b = 2 x c)
Lấy (2) trừ (3) theo vế ta có :
a + 5 x b - (a + 3 x c) = 46 - 18
=> (a - a) + 5 x b - 3 x c = 28
=> 5 x (2 x c) - 3 x c = 28 (Vì b = 2 x c)
=> 10 x c - 3 x c = 28
=> 7 x c = 28
=> c = 4
=> b = 2 x 4 = 8
=> a = 18 - 4 - 8 = 6
Vậy số tờ tiền 2000 là 6
số tờ tiền 5000 là 8
số tờ tiền 10000 là 4