Cho A(x) = -3x2 + x3 - 7x + a và B(x) = x - 5
Tìm a biết rằng số dư của A (x) : B (x) là 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2021
a: \(\Leftrightarrow2x^2+8x+\left(a-8\right)x+4\left(a-8\right)-4a+28⋮x+4\)
hay a=7
CM
12 tháng 7 2017
Để x 3 + ax + b chia cho x + 1 dư 7 thì b – a – 1 = 7 ó -a + b = 8 (1)
Để x 3 + ax + b chia cho x – 3 dư -5 thì b + 3a + 27 = -5 ó 3a + b = -32 (2)
Từ (1) và (2) ta có hệ - a + b = 8 3 a + b = - 32 ó a = - 10 b = - 2
Vậy a = -10, b = -2
Đáp án cần chọn là: C
Bài 1.
CM
30 tháng 10 2017
Vì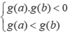 
Do đó đường thẳng y = 0 cắt đồ thị hàm số g(x) tại ba điểm phân biệt có hoành độ 
Vì vậy g(f(x)0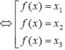 
Hàm số f(x) có 
đồng biến trên R do đó mỗi phương trình 
có một nghiệm thực duy nhất.
Vậy phương trình đã cho có 3 nghiệm thực.
Chọn đáp án A.
\(A\left(x\right)=x^3-3x^2-7x+a\)
\(=x^3-3x^2-7x-15+a+15\)
\(=\left(x-5\right)\left(x^2+2x+3\right)+a+15\)
\(\Rightarrow A\left(x\right)\) chia B(x) dư \(a+15\)
\(\Rightarrow a+15=7\Rightarrow a=-8\)