27x2×x+69x2+36x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
a.
\(\Leftrightarrow\left(3x-1\right)^3=\left(-\dfrac{1}{2}\right)^3\)
\(\Leftrightarrow3x-1=-\dfrac{1}{2}\)
\(\Leftrightarrow3x=\dfrac{1}{2}\)
\(\Leftrightarrow x=\dfrac{1}{6}\)
b.
\(\Leftrightarrow\left(2x-1\right)\left(x-4\right)-x\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(2x-1-x\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\\\end{matrix}\right.\)
c.
\(\Leftrightarrow3x\left(5x-2\right)-2\left(5x-2\right)=0\)
\(\Leftrightarrow\left(3x-2\right)\left(5x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=\dfrac{2}{5}\end{matrix}\right.\)
17 tháng 6 2017
\(\sqrt{81x^2}-8x=\sqrt{\left(9x\right)^2}-8x=\left|9x\right|-8x=9x-8x=x\) ( vì x > 0)
\(6.\sqrt{36x^2}-36x=6.\sqrt{\left(6x\right)^2}-36x=6.\left|6x\right|-36x=6.\left(-6x\right)-36x=-36x-36x=-72x\) (vì x < 0)
3 tháng 3 2022
\(x^2+36x-10=0\\ \Leftrightarrow x\left(x+26\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-26\end{matrix}\right.\)
3 tháng 3 2022
\(\Leftrightarrow x^2+36x+324-334=0\)
\(\Leftrightarrow\left(x+18\right)^2=334\)
hay \(x\in\left\{\sqrt{334}-18;-\sqrt{334}-18\right\}\)
KV
27 tháng 12 2022
2x³ - 22x² + 36x = 0
2x(x² - 11x + 18) = 0
2x(x² - 2x - 9x + 18) = 0
2x[(x² - 2x) - (9x - 18)] = 0
2x[x(x - 2) - 9(x - 2)] = 0
2x(x - 2)(x - 9) = 0
2x = 0 hoặc x - 2 = 0 hoặc x - 9 = 0
*) 2x = 0
x = 0
*) x - 2 = 0
x = 2
*) x - 9 = 0
x = 9
Vậy x = 0; x = 2; x = 9
VT
0
NC
2
28 tháng 10 2021
\(a,\Leftrightarrow\left(x+3\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-12x+36\right)=0\\ \Leftrightarrow x\left(x-6\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
KJ
28 tháng 10 2021
a, (x+3)2 - ( 2x + 1 ).( x+3)=0 b, x3-12x2+36x =0
=> (x+3).(x+3-2x-1) => x(x2-12x+36) = 0
=>(x+3).(-x+2) => x(x-6)2 = 0
=> x+3=0 <=> x=-3 => x=0 <=> x=0
-x+2=0 <=> x=-2 x-6= 0 <=> x=6
KK
4
XO
31 tháng 7 2023
a) (2x - 5)2 - (5 + 2x) = 0
<=> 4x2 - 22x + 20 = 0
\(\Leftrightarrow\left(2x-\dfrac{11}{2}\right)^2=\dfrac{41}{4}\)
\(\Leftrightarrow x=\dfrac{\pm\sqrt{41}+11}{4}\)
b) \(27x^3-54x^2+36x=0\)
\(\Leftrightarrow x\left(3x^2-6x+4\right)=0\)
\(\Leftrightarrow x=0\) (Vì \(3x^2-6x+4=3\left(x-1\right)^2+1>0\forall x\))
c) x3 + 8 - (x + 2).(x - 4) = 0
\(\Leftrightarrow\left(x+2\right).\left(x^2-2x+4\right)-\left(x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-3x+8\right)=0\)
\(\Leftrightarrow x=-2\) (Vì \(x^2-3x+8=\left(x-\dfrac{3}{2}\right)^2+\dfrac{23}{4}>0\))
d) \(x^6-1=0\)
\(\Leftrightarrow\left(x^2\right)^3-1=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\)
\(\Leftrightarrow x^2-1=0\) (Vì \(x^4+x^2+1>0\))
\(\Leftrightarrow x=\pm1\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
\(d,x^6-1=0\\ \Leftrightarrow\left(x^2\right)^3-1^3=0\\ \Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x^4+x^2+1=0\left(Vô.lí,vì:x^4\ge0;x^2\ge0,\forall x\in R\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ c,\left(x^3+8\right)-\left(x+2\right)\left(x-4\right)=0\\ \Leftrightarrow\left(x^3+8\right)-\left(x^2-2x-8\right)=0\\ \Leftrightarrow x^3-x^2+2x+16=0\\ \Leftrightarrow x^3+2x^2-3x^2-6x+8x+16=0\\ \Leftrightarrow x^2\left(x+2\right)-3x\left(x+2\right)+8\left(x+2\right)=0\\ \Leftrightarrow\left(x^2-3x+8\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-3x+8=0\left(Vô.lí\right)\\x+2=0\end{matrix}\right.\Leftrightarrow x=-2\)
YE
1
27 tháng 1 2017
36x - x2 = 0
<=> x(36 - x) = 0
<=> x = 0 hoặc 36 - x = 0
<=> x = 0 hoặc x = 36
Vậy x = 0 hoặc x = 36
ung ho minh len 200 nha
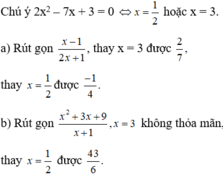
Đề ko có vấn đề chứ ạ ?
\(27x^2.x+69x^2+36x=0\)
Tương đương vs pt : \(\Leftrightarrow27x^3+69x^2+36x=0\)
\(\Leftrightarrow3x\left(9x^2+23x+12\right)=0\)
TH1 : \(3x=0\Leftrightarrow x=0\)
TH2 : \(\Delta=23^2-4.12.9=529-432=97>0\)
Phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-23-\sqrt{97}}{3};x_2=\frac{-23+\sqrt{97}}{3}\)