Cho (O) có 2 đường kính AB & CD ⊥ với nhau. Đ' E ϵ OC ( E # O, C ). nối AE cắt (O) tại M
a, CMR : AC2 = AE . AM
b, xác định vị trí của E trên OC để MA = 2MB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 12 2023
Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC
13 tháng 6 2023
góc AEB=1/2*180=90 độ
góc CDA=1/2*180=90 độ
góc CEB=góc CDB
=>CDEB nội tiếp
CM
19 tháng 5 2017
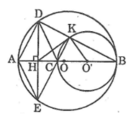
Vì O, O’ và B thẳng hàng nên: O’B < OB => O’ nằm giữa O và B
Ta có: OO’ = OB - O’B
Vậy đường tròn (O’) tiếp xúc với đường tròn (O) tại B
12 tháng 9 2019
https://olm.vn/hoi-dap/detail/66015664055.html bạn vào đây tham khảo nha
CM
22 tháng 11 2018
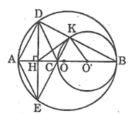
Tam giác DEK vuông tại K có KH là trung tuyến thuộc cạnh huyền DE nên: HK = HE = (1/2).DE (tính chất tam giác vuông)
Suy ra tam giác EHK cân tại H
CM
19 tháng 2 2017
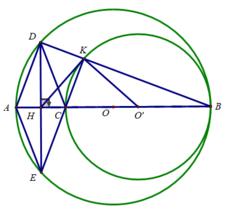
d) Xét tam giác DEK vuông tại K có KH là trung tuyến nên KH = HE
ΔKHE có KH = HE ⇒ ΔKHE cân tại H
⇒ ∠(HKE ) = ∠(KEH)
Lại có ΔO'CK cân tại O' ⇒ ∠(O'CK) = (O'KC)
⇒ ∠(HKE ) + ∠(O'KC) = ∠(KEH) + ∠(O'CK)
⇔ ∠(O'KH) = ∠(KEH) + ∠(O'CK)
Mặt khác ∠(O'CK) = ∠(HCE) (đối đỉnh)
ΔHEC vuông tại H nên ∠(KEH) + ∠(HCE) = 90o ⇒ ∠(KEH) + ∠(O'CK) = 90 0
Hay ∠(O'KH) = 90 0
⇒ KH là tiếp tuyến của (O')