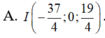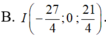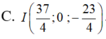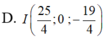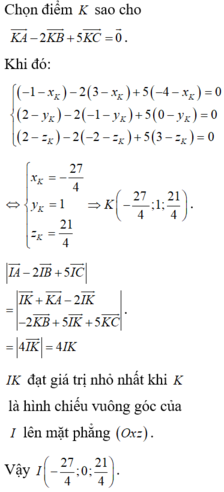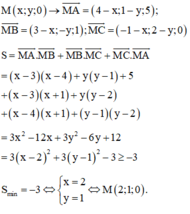tìm tọa độ điểm I thuộc đt AM sao cho vecto AI *(BA-IB) đạt giá trị nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi `M(x;3/2x+5/2)`
Ta có:`|\vec{MA}-2\vec{MB}|`
`=|(4-x;7-3/2x-5/2)-2(2-x;1-3/2x-5/2)|`
`=|(x;3/2x+17/2)|`
`=\sqrt{x^2+(3/2x+17/2)^2}`
`=\sqrt{x^2+9/4x^2+51/2x+289/4}`
`=\sqrt{13/4x^2+51/2x+289/4}`
`=\sqrt{(\sqrt{13}/2 x+[51\sqrt{13}]/26)^2+289/13} >= [17\sqrt{13}]/13`
Dấu "`=`" xảy ra `<=>\sqrt{13}/2x+[51\sqrt{13}]/26=0<=>x=-51/13`
`=>M(-51/13;-44/13)`

Đáp án B.
Gọi M là điểm thỏa mãn
M A → − 2 M B → + 5 M C → = 0 ⇔ M − 27 4 ; 1 ; 21 4
Khi đó
I A → − 2 I B → + 5 I C → = I M → + M A → − 2 I M → + 5 I M → + 5 M C → = 4 I M → + 0 → = 4 I M →
Biểu thức I A → − 2 I B → + 5 I C → đạt giá trị nhỏ nhất ⇔ I M → nhỏ nhất => I là hình chiếu của M trên mặt phẳng O x z ⇔ I − 27 4 ; 0 ; 21 4 .
Bài toán tổng quát: Trong không gian cho các điểm A 1 , A 2 ,..., A n và mặt phẳng P . Tìm điểm I trên mặt phẳng P sao cho biểu thức k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → đạt giá trị nhỏ nhất, trong đó k 1 , k 2 ,..., k n là những số thực và ∑ i = 0 n k i ≠ 0 .
Cách giải:
- Tìm điểm M thỏa mãn k 1 M A 1 → + k 2 M A 2 → + ... + k n M A n → = 0 .
- Khi đó k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → = ∑ i = 1 n k i I M → .
- Do đó k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → đạt giá trị nhỏ nhất ⇔ I M → nhỏ nhất => I là hình chiếu vuông góc của M trên P .

\(\overrightarrow{AB}=\left(-6;-3\right)=-3\left(2;1\right)\Rightarrow\) đường thẳng AB nhận \(\left(2;1\right)\) là 1 vtcp
Phương trình tham số đường thẳng AB có dạng: \(\left\{{}\begin{matrix}x=5+2t\\y=4+t\end{matrix}\right.\)
Do M thuộc AB nên tọa độ M có dạng \(M\left(5+2t;4+t\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-2t;-t\right)\\\overrightarrow{MC}=\left(-2-2t;-6-t\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MC}=\left(-2-4t;-6-2t\right)\)
Đặt \(T=\left|\overrightarrow{MA}+\overrightarrow{MC}\right|=\sqrt{\left(-2-4t\right)^2+\left(-6-2t\right)^2}=\sqrt{20\left(t+1\right)^2+20}\ge\sqrt{20}\)
Dấu "=" xảy ra khi \(t+1=0\Rightarrow t=-1\Rightarrow M\left(3;3\right)\)

Đáp án D
Gọi I x I ; y I ; z I thỏa mãn điều kiện 3 I A ¯ + 2 I B ¯ − I C ¯ = 0 ¯ ⇒ I − 3 4 ; 1 2 ; − 1
Ta có P = 3 M A 2 + 2 M B 2 − M C 2 = 3 M I ¯ + I A ¯ 2 + 2 M I → + I B ¯ 2 − M I ¯ + I C ¯ 2
= 4 M I 2 + 2 M I ¯ 3 I A ¯ + 2 I B ¯ − I C ¯ ⏟ 0 + 3 I A 2 + 2 I B 2 − I C 2 = 4 M I 2 + 3 I A 2 + 2 I B 2 − I C 2
Suy ra P min ⇔ M I min ⇒ M trùng với điểm I. Vậy M − 3 4 ; 1 2 ; − 1

Đáp án D
Gọi I ( x I ; y I ; z I ) thỏa mãn điều kiện
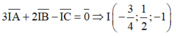
Ta có
![]()
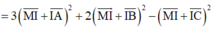
![]()
![]()
![]()
=> M trùng với điểm I. Vậy M = - 3 4 ; 1 2 ; - 1

I B A C M D
Đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=25\) có tâm \(I\left(1;1\right)\) và bán kính \(R=5\)
\(\overrightarrow{IA}=\left(6;8\right)\Rightarrow IA=10=2R\)=> Đường tròn (C) chia đôi IA tại C
Gọi D là trung điểm IC, ta có: \(\frac{ID}{IM}=\frac{1}{2}=\frac{IM}{IA}\)=> \(\Delta\)IDM ~ \(\Delta\)IMA (c.g.c), từ đây MA=2MD
Suy ra \(P=2\left(MD+MB\right)\ge2BD\)(không đổi)
Dấu "=" xảy ra khi M thuộc đoạn BD hay M là giao điểm của đoạn BD với (C)
*) Tìm M:
Ta có: C là trung điểm IA => \(C\left(4;5\right)\), D là trung điểm IC => \(D\left(\frac{5}{2};3\right)\)
\(\overrightarrow{BD}=\left(\frac{5}{2};-5\right)\Rightarrow BD:\hept{\begin{cases}x=\frac{5}{2}t\\y=8-5t\end{cases}}\); vì M thuộc BD nên \(M\left(\frac{5}{2}t;8-5t\right)\)
\(\overrightarrow{IM}=\left(\frac{5}{2}t-1;7-5t\right)\Rightarrow IM^2=\left(\frac{5}{2}t-1\right)^2+\left(7-5t\right)^2=R^2=25\)
\(\Leftrightarrow\orbr{\begin{cases}t=2\\t=\frac{2}{5}\end{cases}}\Rightarrow\orbr{\begin{cases}M\left(5;-2\right)\\M\left(1;6\right)\end{cases}}\)
Nếu \(M\left(5;-2\right)\)thì \(\overrightarrow{MB}=\left(-5;10\right);\overrightarrow{MD}=\left(-\frac{5}{2};5\right)\Rightarrow\overrightarrow{MB}=2\overrightarrow{MD}\)=> M nằm ngoài đoạn BD (L)
Vậy \(M\left(1;6\right)\).