Dạng 2: Vận dụng công thức tính vận tốc và vận tốc trung bình
Câu 2: Hai người đi xe đạp. Người thứ nhất đi quãng đường 300m hết 1 phút. Người thứ hai
đi quãng đường 7,5km hết 0,5h. Hãy tính vận tốc của mỗi người và so sánh người nào đi
nhanh hơn?
Câu 3: Một ô tô chuyển động đều với vận tốc v1 = 30km/h trên đoạn đường AM dài 60km.
Sau đó, ô tô tiếp tục chuyển động đều với vận tốc v2 = 40km/h trên đoạn MB dài 120km. Tính
vận tốc trung bình của chuyển động trên cả quãng đường từ AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc người thứ nhất đi là : `300m//p = 0,3 km//p = 18km//h`.
Vận tốc người thứ hai là: `7,5km//0,5h = 15km//h`.
Vì `18km//h > 15 km//h ->` Vận tốc người thứ nhất sẽ nhanh hơn vận tốc người thứ hai.

Đổi \(10p=\dfrac{1}{6}\left(h\right)\)
a) Vận tốc của người I là:
\(v_1=\dfrac{s_1}{t_1}=\dfrac{3}{\dfrac{1}{6}}=18\left(km.h\right)\)
Vận tốc của người II là:
\(v_2=\dfrac{s_2}{t_2}=\dfrac{7,5}{0,5}=15\left(km.h\right)\)
b) Người thứ nhất đi nhanh hơn vì có vận tốc lớn hơn (18>15)

\(\left\{{}\begin{matrix}v'=s':t'=300:60=5\left(\dfrac{m}{s}\right)=18\left(\dfrac{km}{h}\right)\\v''=s'':t''=7,5:0,5=15\left(\dfrac{km}{h}\right)\\v=\dfrac{s'+s''}{t'+t''}=\dfrac{\left(300:1000\right)+7,5}{\dfrac{1}{60}+0,5}\approx15,1\left(\dfrac{km}{h}\right)\end{matrix}\right.\)

Vận tốc người thứ nhất:
\(v_1=\dfrac{S_1}{t_1}=\dfrac{600}{2\cdot60}=5\)m/s
Vận tốc người thứ hai:
\(v_2=\dfrac{S_2}{t_2}=\dfrac{8}{0,5}=16\)km/h\(=\dfrac{40}{9}\approx4,44\)m/s
Vậy người thứ nhất di nhanh hơn.

Vận tốc của người thứ nhất là:
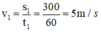
Vận tốc của người thứ hai là:
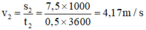
Vì v1 > v2 nên người thứ nhất đi nhanh hơn người thứ hai.

Bài 1: Tóm tắt
\(S_1=24km\)
\(V_1=12km\)/\(h\)
\(S_2=12km\)
\(V_2=45'=0,75h\)
_______________
a) \(t_1=?\)
b) \(V_{TB}\)
Giải
a) Thời gian người đó đạp xe trên quãng đường đầu là: \(t_1=\frac{S_1}{V_1}=\frac{24}{12}=2\left(h\right)\)
b) Ta có công thức tính vận tốc trung bình là: \(V=\frac{S_1+S_2+....+S_n}{t_1+t_2+t_3+....+t_n}\)
Vậy vận tốc trung bình của người đó trên quãng đường là:
\(V_{TB}=\frac{S_1+S_2}{t_1+t_2}=\frac{24+12}{2+0,75}\approx13\)(km/h)
Bài 2: Tóm tắt
\(S_1=600m=0,6km\)
\(t_1=2'=\frac{1}{30}\left(h\right)\)
\(S_2=10,8km\)
\(t_2=0,75h\)
_________________
a) \(V_1=?;V_2=?\)
b) \(S_{KC}=?\)
Giải
a) Vận tốc của người thứ nhất là: \(V_1=\frac{S_1}{t_1}=\frac{0,6}{\frac{1}{30}}=18\)(km/h)
Vận tốc của người thứ 2 là: \(V_2=\frac{S_2}{t_2}=\frac{10,8}{0,75}=14,4\) (km/h)
=> Người thứ nhất đi nhanh hơn người thứ 2.
b) Do đi cùng lúc => thời gian đi của 2 người là như nhau và vận tốc đã cho
=> Hai người cách nhau số km là: \(S-t\left(V_1+V_2\right)=S-\frac{1}{3}\left(18+14,4\right)=S-10,8\)
Theo đề thì còn cần phải dựa vào khoảng cách của 2 người khi 2 người bắt đầu đi nữa.
a) Thời gian người đó đạp xe trên quãng đường thứ nhất là :
24 : 12 = 2 (giờ)
b) Đổi : 45 phút = 0,75 giờ
=> Vận tốc trung bình của người đi xe đạp trên cả quãng đường là :
(S1 + S2) / (t1 + t2) = (12+24) / (2+0,75) = 13 (km/h)

V quãng đường thứ hai là:
90min/18km=5km/h
Vận tốc của người đi xe đạp trên cả quãng đường là:
(5+15):2=10km/h
Vậy vận tốc của người đi xe đạp trên cả quãng đường là: 10km/h
Câu 2: Đổi: \(1ph=60s\)
\(\left\{{}\begin{matrix}v_1=\dfrac{S_1}{t_1}=\dfrac{300}{60}=5\left(m/s\right)=18\left(km/h\right)\\v_2=\dfrac{S_2}{t_2}=\dfrac{7,5}{0,5}=15\left(km/h\right)\end{matrix}\right.\)
\(v_1>v_2\left(18>15\right)\Rightarrow\) Người thứ 1 đi nhanh hơn
Câu 3:
\(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{60}{30}=2\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{120}{40}=3\left(h\right)\end{matrix}\right.\)
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{60+120}{2+3}=36\left(km/h\right)\)