Với a, b,c là các số cho trước, giải phương trình sau:
x3 – (a + b + c)x2 = - (ab + ac + bc)x + abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
19 tháng 6 2022
\(a)\) ĐKXĐ: \(a\ne-b;a\ne-c;b\ne-c\)
\(\dfrac{x-ab}{a+b}+\dfrac{x-ac}{a+c}+\dfrac{x-bc}{b+c}=a+b+c\)
\(\Leftrightarrow\left(\dfrac{x-ab}{a+b}-c\right)+\left(\dfrac{x-ac}{a+c}-b\right)+\left(\dfrac{x-bc}{b+c}-a\right)=0\)
\(\Leftrightarrow\dfrac{x-ab-ac-bc}{a+b}+\dfrac{x-ac-ab-bc}{a+c}+\dfrac{x-bc-ab-ac}{b+c}=0\)
\(\Leftrightarrow\left(x-ab-ac-bc\right)\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)=0\)
Vì \(a,b,c>0\Rightarrow\dfrac{1}{a+b}+\dfrac{1}{a+c}+\dfrac{1}{b+c}>0\)
\(\Leftrightarrow x-ab-ac-bc=0\)
\(\Leftrightarrow x=ab+ac+bc\)
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
CM
16 tháng 12 2018
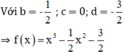
a) f’(x) = 3x2 – x.
⇒ f’(-1) = 4; f(-1) = -3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -1 là:
y = 4.(x + 1) – 3 = 4x + 1.
b) f’(sin x) = 0
⇔ 3.sin2x – sin x = 0
⇔ sin x.(3sin x – 1) = 0
3 tháng 4 2020
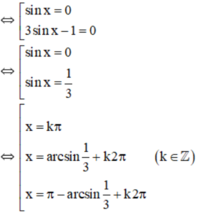
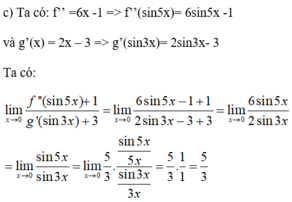
Giải và biện luận các phương trình sau
a) (x-ab)/(a+b) + (x-ac)/(a+c) + (x-bc)/(b+c) = a+b+c
b) (x-a)/bc + (x-b)/ac + (x-c)/ab = 2(1/a + 1/b + 1/c)
CM
2 tháng 10 2019
Phương trình x2 + (a + b + c)x + (ab + bc + ca) = 0
Có Δ = (a + b + c)2 − 4(ab + bc + ca)
= a2 + b2 + c2 – 2ab – 2bc – 2ac
= (a – b)2 – c2 + (b – c)2 – a2 + (a – c)2 – b2
= (a – b – c)(a + c – b) + (b – c – a)
(a + b – c) + (a – c – b)(a – c + b)
Mà a, b, c là ba cạnh của một tam giác nên
a − b − c < 0 b − c − a < 0 a − c − b < 0 ; a + c − b > 0 a + b − c > 0
Nên Δ < 0 với mọi a, b, c
Hay phương trình luôn vô nghiệm với mọi a, b, c
Đáp án cần chọn là: D
TH
1
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
PT $\Leftrightarrow 3x-\left(\frac{ab}{a+b}+\frac{bc}{b+c}+\frac{ac}{a+c}\right)=a+b+c$
$\Leftrightarrow 3x=\frac{ab}{a+b}+\frac{bc}{b+c}+\frac{ca}{c+a}+a+b+c$
$=(ab+bc+ac)(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a})$
$\Leftrightarrow x=\frac{1}{3}(ab+bc+ac)(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a})$
3 tháng 4 2020
Cho abc(a+b+c) khác 0. Giải phương trình ẩn x:
(x-a)/bc+(x-b)/ac+(x-c)/ab=1/2(1/a+1/b+1/c)
.
Chắc ko phải cách khác đâu, mà là chi tiết thôi :))
Cách khác:
x3 - (a + b + c)x2 = -(ab + ac + bc)x + abc
\(\Leftrightarrow\) x3 - (a + b + c)x2 + (ab + ac + bc)x - abc = 0
\(\Leftrightarrow\) x3 - ax2 + bx2 + cx2 + abx + acx + bcx - abc = 0
\(\Leftrightarrow\) (x3 - ax2) - (bx2 - abx) - (cx2 - cax) + (bcx - abc) = 0
\(\Leftrightarrow\) x2(x - a) - bx(x - a) - cx(x - a) + bc(x - a) = 0
\(\Leftrightarrow\) (x - a)[(x2 - bx) - (cx - bc)] = 0
\(\Leftrightarrow\) (x - a)[x(x - b) - c(x - b)] = 0
\(\Leftrightarrow\) (x - a)(x - b)(x - c) = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x-a=0\\x-b=0\\x-c=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=a\\x=b\\x=c\end{matrix}\right.\)
Vậy S = {a; b; c}
Chúc bn học tốt!!