giúp em bài này ạ em săp thi r giúp em
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
N
NguyễnLýHải
24 tháng 10 2021
Tập hợp các chữ số của số 2022 là
Đúng(0)
Những câu hỏi liên quan
KH
0
LH
2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2024
2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2024
3.
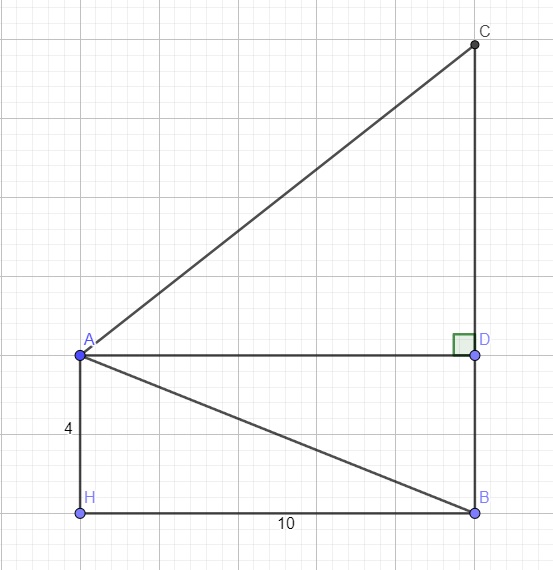
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)
13 tháng 3 2022
1 Tet Nguyen Dan
2 Yes,is it
3 It begin between January twenty -first and February nineteen
4 They tidy their houses,cook special foods,clean and make offerings on the family altars
5 To see New Year in
LH
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2024
a.
D E thuộc Ox \(\Rightarrow\) tọa độ E có dạng \(E\left(x;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OE}=\left(x;0\right)\\\overrightarrow{OM}=\left(4;1\right)\end{matrix}\right.\)
Tam giác OEM cân tại O \(\Rightarrow OE=OM\)
\(\Rightarrow\sqrt{x^2+0^2}=\sqrt{4^2+1^2}\Rightarrow x^2=17\)
\(\Rightarrow x=\pm\sqrt{17}\Rightarrow\left[{}\begin{matrix}E\left(\sqrt{17};0\right)\\E\left(-\sqrt{17};0\right)\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-4;-1\right)\\\overrightarrow{MB}=\left(-4;b-1\right)\end{matrix}\right.\)
Tam giác ABM vuông tại M \(\Rightarrow\overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Rightarrow-4\left(a-4\right)-1\left(b-1\right)=0\)
\(\Leftrightarrow4a+b-17=0\Rightarrow b=17-4a\)
Lại có \(S_{ABM}=\dfrac{1}{2}MA.MB=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(b-1\right)^2+16}\)
\(=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(16-4a\right)^2+16}=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{16\left[\left(a-4\right)^2+1\right]}\)
\(=2\left[\left(a-4\right)^2+1\right]\ge2\)
Dấu "=" xảy ra khi \(a-4=0\Rightarrow a=4\Rightarrow b=1\)
1 tháng 3 2019
chụy ko cần sự giúp đỡ vô duyên thúi của em nha
LT
1
HT
30 tháng 4 2021
1/ \(B=2.10^{-7}.\dfrac{I}{r}=2.10^{-7}.\dfrac{10}{0,4}=5.10^{-6}\left(T\right)\)
2/ \(L=4\pi.10^{-7}.\dfrac{N^2}{l}.S=4\pi.10^{-7}.\dfrac{1000^2}{0,628}.100.10^{-4}=6,4\pi.10^{-3}\left(H\right)\)
\(\xi_{tc}=\dfrac{L.\Delta i}{\Delta t}=6,4\pi10^{-3}.4.\dfrac{1}{0,2}=128\pi.10^{-3}\left(V\right)\)
3/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{10}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=15\left(cm\right)\)
\(k=-\dfrac{d'}{d}=-\dfrac{15}{30}=-\dfrac{1}{2}\)
\(A'B'=\left|k\right|AB=\dfrac{1}{2}.2=1\left(cm\right)\)
Ảnh thật, ngược chiều,nhỏ hơn vật
P/s: Bạn tự vẽ hình
LT
1
HT
30 tháng 4 2021
1/ \(B=2\pi.10^{-7}.\dfrac{NI}{r}\Rightarrow I=\dfrac{B.r}{2\pi.10^{-7}.N}=\dfrac{6,28.10^{-6}.0,05}{2\pi.10^{-7}.100}=...\left(A\right)\)
2/ \(\phi=NBS\cos\alpha=500.0,4.4.10^{-3}.\cos0^0=0,8\left(Wb\right)\)
b/ \(\xi=\dfrac{\Delta\phi}{\Delta t}=\dfrac{2.0,8-0,8}{0,02}=40\left(V\right)\)
3/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow-\dfrac{1}{20}=\dfrac{1}{20}+\dfrac{1}{d'}\Rightarrow d'=-10\left(cm\right)\)
\(\Rightarrow k=-\dfrac{d'}{d}=\dfrac{10}{20}=\dfrac{1}{2}\Rightarrow A'B'=\left|k\right|AB=\dfrac{1}{2}.AB\)
Anh ao, cung chieu, bang mot nua vat
P/s: Ban tu ve hinh