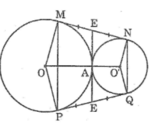
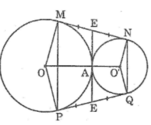
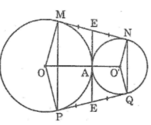
cho hai đường tròn o và o tiếp xúc ngoài tại a. kẻ tiếp tuyến chung ngoiaf mn với m thuộc (O) và n thuộc (O'). gọi p là điểm đối xứng với m qua oo', q là điểm đối xứng với n qua oo'.chứng minh
a)mnpq là hình thang cân
b) PQ là tếp tuyến chung của hai đường tròn (O) và (O')
MN + PQ = MP + NQ