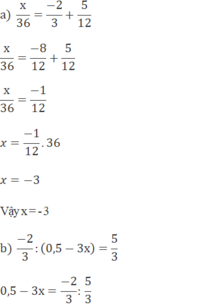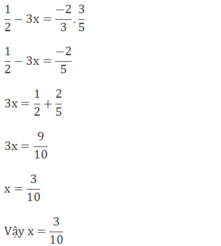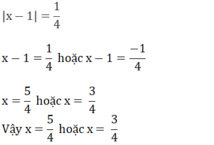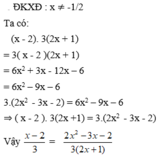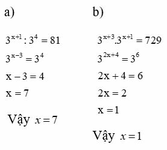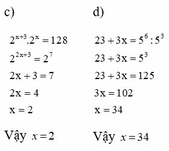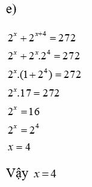3x+1+23=2.25.1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


<=> 75x+23 = 3x-1 or 75x+23 = -(3x-1)
<=> x = -1/3 or x = -11/39

\(\Leftrightarrow\frac{3x+1}{17}+\frac{3x+1}{19}+\frac{3x+1}{23}-\frac{3x+1}{29}-\frac{3x+1}{31}=0\)
\(\Leftrightarrow\left(3x+1\right)\left(\frac{1}{17}+\frac{1}{19}+\frac{1}{23}-\frac{1}{29}-\frac{1}{31}\right)=0\)
\(\Leftrightarrow3x+1=0\) ( vì \(\frac{1}{17}+\frac{1}{19}+\frac{1}{23}-\frac{1}{29}-\frac{1}{31}\ne0\))
\(\Leftrightarrow3x=-1\)
\(\Leftrightarrow x=-\frac{1}{3}\)
\(\frac{3x+1}{17}+\frac{3x+1}{19}+\frac{3x+1}{23}=\frac{3x+1}{29}+\frac{3x+1}{31}\)
\(\Rightarrow\frac{3x+1}{17}+\frac{3x+1}{19}+\frac{3x+1}{23}-\frac{3x+1}{29}-\frac{3x+1}{31}=0\)
\(\Rightarrow\left(3x+1\right)\left(\frac{1}{17}+\frac{1}{19}+\frac{1}{23}-\frac{1}{29}-\frac{1}{31}\right)=0\)
Mà \(\frac{1}{17}+\frac{1}{19}+\frac{1}{23}-\frac{1}{29}-\frac{1}{31}\ne0\)
\(\Rightarrow3x+1=0\)
\(\Rightarrow x=-\frac{1}{3}\)

a,(2x-1)3 =23+102 b,(3x+1)+(3x+3)+...+(3x+99)=2800
(2x-1)3 =125 3x+1+3x+3+...+3x+99=2800
(2x-1)3=53 ( 3x+3x+.....+3x )+(1+3+...+99)=2800
2x-1=5 gọi A=3x+3x+...+3x ; B=1+3+...+99
2x=5+1 số số hạng của B là : (99-1):2+1=50 ( bằng số số hạng của A)
2x=6 B = (99+1) x 50:2
=2500
x=6:2 ta có: 150x + 2500=2800
x=3 150x=2800-2500
vậy x=3 150x=300
x=300:150
x=2
vậy x=2

\(a,x-5\left(x-2\right)=6x\\ \Leftrightarrow x-5x+10-6x=0\\ \Leftrightarrow-10x+10=0\\ \Leftrightarrow x=1\\ b,2^3+3x^2-32x=48\\ \Leftrightarrow3x^2-32x+8=48\\ \Leftrightarrow3x^2-32x-40=0\)
Nghiệm xấu lắm bn
\(c,\left(3x+1\right)\left(x-3\right)^2=\left(3x+1\right)\left(2x-5\right)^2\\ \Leftrightarrow c,\left(3x+1\right)\left[\left(2x-5\right)^2-\left(x-3\right)^2\right]\\ \Leftrightarrow\left(3x+1\right)\left(2x-5-x+3\right)\left(2x-5+x-3\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(x-2\right)\left(3x-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=2\\x=\dfrac{8}{3}\end{matrix}\right.\)
\(d,9x^2-1=\left(3x+1\right)\left(4x+1\right)\\ \Leftrightarrow\left(3x+1\right)\left(4x+1\right)-\left(3x-1\right)\left(3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(4x+1-3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-2\end{matrix}\right.\)
\(b,2x^3+3x^2-32x-48=0\\ \Leftrightarrow\left(2x^3-8x^2\right)+\left(11x^2-44x\right)+\left(12x-48\right)=0\\ \Leftrightarrow2x^2\left(x-4\right)+11x\left(x-4\right)+12\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(2x^2+11x+12\right)=0\\ \Leftrightarrow\left(x-4\right)\left[\left(2x^2+8x\right)+\left(3x+12\right)\right]=0\\ \Leftrightarrow\left(x-4\right)\left[2x\left(x+4\right)+3\left(x+4\right)\right]=0\\ \Leftrightarrow\left(x-4\right)\left(2x+3\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{3}{2}\\x=-4\end{matrix}\right.\)

\(3^{x-1}.7+3^{x-1}.2=9\\ 3^{x-1}.\left(7+2\right)=9\\ 3^{x-1}.9=9\\ 3^{x-1}=\dfrac{9}{9}=1\\ Mà:3^0=1\\ Nên:x-1=0\\ Vậy:x=0+1=1\\ ---\\ P=2+2^2+2^3+...+2^{65}+2^{66}=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{64}+2^{65}+2^{66}\right)\\ =2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{64}\left(1+2+2^2\right)\\ =2.7+2^4.7+...+2^{64}.7\\ =\left(2+2^4+....+2^{64}\right).7⋮7\left(đpcm\right)\)
+)
\(3^{x-1}.7+3^{x-1}.2=9\)
\(3^{x-1}.\left(7+2\right)=9\)
\(3^{x-1}.9=9\)
\(3^{x-1}=9:9\)
\(3^{x-1}=1\)
⇔\(3^{x-1}=3^0\)
⇒\(x-1=0\)
\(x=0+1\)
\(x=1\)
Vậy \(x=1\)
+)
\(2+2^2+2^3+...+2^{65}+2^{66}\)
Vì \(2+2^2+2^3=14\) mà \(14\)⋮\(7\)
⇒Ta nhóm 3 số với nhau
Ta có:
\(\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{64}+2^{65}+2^{66}\right)\)
\(\left(2+2^2+2^3\right)+2^3.\left(2+2^2+2^3\right)+...+2^{63}.\left(2+2^2+2^3\right)\)
\(14.1+14.2^3+...+14.2^{63}\)
\(14.\left(1+2^3+...+2^{63}\right)\)
Do \(14\)⋮\(7\) nên \(P=14.\left(2+2^3+...+2^{63}\right)\)⋮\(7\)
Xin tick