Cho Oy, OxOy,Ox lần lượt là tia phân giác của hai góc kề bù \widehat{nOm},\widehat{mOz}nOm,mOz. Tính số đo góc \widehat{yOx}yOx.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
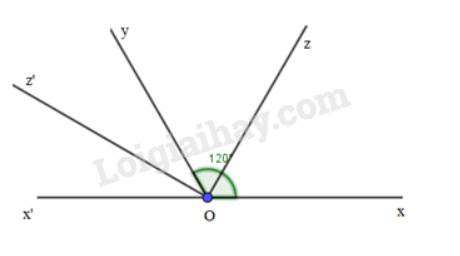
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
NM
13 tháng 4 2021
Trả lời:
góc x'Om= 55+70 =125 độ
góc xOn= 110+35 =145 độ
góc nOm= 35+55= 90 độ
13 tháng 4 2021
Vì 2 góc xoy và yox' là hay góc kề bù
=> Tia Oy nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{xOy}+\widehat{yOx'}=\widehat{xOx'}\)
hay \(110^0+\widehat{yOx'}=180^0\)
\(\Rightarrow\widehat{yOx'}=70^0\)
Vì tia Om là tia phân giác của góc xOy ta có :
\(\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=\frac{110^0}{2}=55^0\)
Vì tia On là tia phân giác của góc yOx' ta có :
\(\widehat{yOn}=\widehat{nOx'}=\frac{\widehat{yOx'}}{2}=\frac{70^0}{2}=35^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta có : \(\widehat{xOm}< \widehat{xOx'}\left(55^0< 180^0\right)\)
=> Tia Om nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{xOm}+\widehat{x'Om}=\widehat{xOx'}\)
hay \(55^0+\widehat{x'Om}=180^0\)
\(\Rightarrow\widehat{x'Om}=125^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta có : \(\widehat{nOx'}< \widehat{xOx'}\left(35^0< 180^0\right)\)
=> Tia On nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{nOx}+\widehat{nOx'}=\widehat{xOx'}\)
hay \(\widehat{nOx}+35^0=180^0\)
\(\Rightarrow\widehat{nOx}=145^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta thấy Tia Oy nằm giữa 2 tia Ox và Ox'
hay tia Oy cũng nằm giữa 2 tia Om và On
Ta có :
\(\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
hay \(55^0+35^0=\widehat{mOn}\)
\(\Rightarrow\widehat{mOn}=90^0\)
Vậy \(\widehat{x'Om}=125^0;\)\(\widehat{xOn}=145^0\)và \(\widehat{nOm}=90^0\)
19 tháng 9 2023
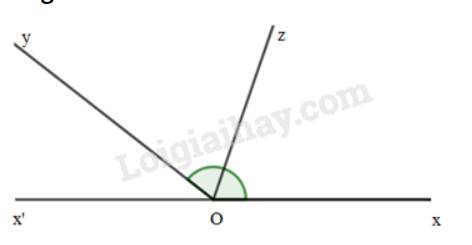
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.142^\circ = 71^\circ \)
Mà \(\widehat {x'Oz}\) và \(\widehat {xOz}\) là 2 góc kề bù nên \(\widehat {xOz} + \widehat {x'Oz} = 180^\circ \Rightarrow 71^\circ + \widehat {x'Oz} = 180^\circ \Rightarrow \widehat {x'Oz} = 180^\circ - 71^\circ = 109^\circ \)
Vậy \(\widehat {x'Oz} = 109^\circ \)
18 tháng 4 2017
Giải:
Hai góc xOy và x'Oy là hai góc kề bù mà = 1000 nên
= 1800 - 1000 = 800.
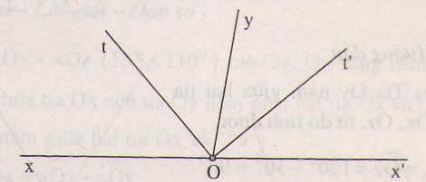
Giải tương tự bài 33, ta được ,
N
31 tháng 7 2019
a) Trên cùng 1 ... chứa tia Ox, có \(\widehat{xOz}=50\text{°}\)và \(\widehat{xOy}=80\text{°}\)
=> \(\widehat{xOz}< \widehat{xOy}\)
=> Tia Oz nằm giữa 2 tia Ox và Oy (1)
=> \(\widehat{zOy}+\widehat{xOz}=\widehat{xOy}\)
Ta thay: \(\widehat{xOz}=50\text{°},\widehat{xOy}=80\text{°}\)
=> \(\widehat{zOy}+50\text{°}=80\text{°}\)
=> \(\widehat{zOy}=80\text{°}-50\text{°}=30\text{°}\)
Ta có: \(\widehat{zOy}< \widehat{xOz}\left(30\text{°}< 50\text{°}\right)\)(2)
Từ (1) và (2) => Tia Oz không phải tia phân giác của \(\widehat{xOy}\)
b) Vì tia Ox' là tia đối của tia Ox nên \(\widehat{xOy}+\widehat{yOx'}=180\text{°}\)(Kề bù)
Ta thay \(\widehat{xOy}=80\text{°}\)
=> \(80\text{°}+\widehat{yOx'}=180\text{°}\)
=> \(\widehat{yOx'}=180\text{°}-80\text{°}=100\text{°}\)
c) Vì tia Om là tia phân giác của \(\widehat{yOx'}\)
=> \(\widehat{mOx'}=\widehat{mOy}=\frac{\widehat{yOx'}}{2}\)
Mà \(\widehat{yOx'}=100\text{°}\)(Ngoặc ''}'' 2 điều lại)
=> \(\widehat{mOx'}=\widehat{mOy}=\frac{100\text{}\text{°}}{2}=50\text{°}\)
Ta có: \(\widehat{mOy}+\widehat{zOy}=\widehat{mOz}\)
Ta thay: \(\widehat{mOy}=50\text{°},\widehat{zOy}=30\text{°}\)
=> \(50\text{°}+30\text{°}=\widehat{mOz}\)
=> \(\widehat{mOz}=80\text{°}\)
P/s: Có gì khó hiểu thì nhắn tin hỏi nhé, còn về nhận xét \(\widehat{mOz}\)thì nghĩ mang máng kiểu:
Ta có: \(\widehat{mOz}=80\text{°}\)và \(\widehat{xOy}=80\text{°}\)
=> \(\widehat{mOz}=\widehat{xOy}\)
Cũng không chắc, viết sao cũng được, nếu muốn thì có thể sửa phần trình bày ^^
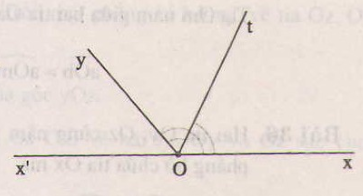
Theo đề bài, ta có \widehat{nOz}=\frac{1}{2}\widehat{xOz},\widehat{mOz}=\frac{1}{2}\widehat{zOy}nOz=21xOz,mOz=21zOy.
Mặt khác, \widehat{xOz},\widehat{zOy}xOz,zOy là hai góc kề bù nên \widehat{xOz}+\widehat{zOy}=180^o.xOz+zOy=180o.
Do đó \widehat{nOm}=\widehat{nOz}+\widehat{mOz}=\frac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=90^onOm=nOz+mOz=21(xOz+yOz)=90o.