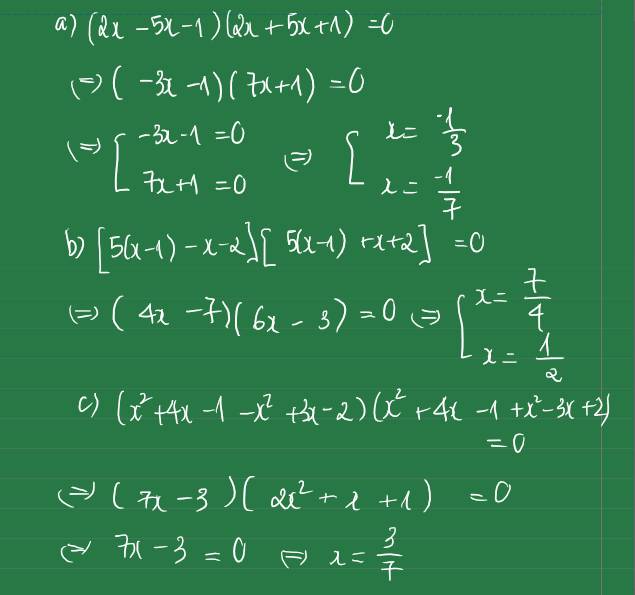giải phương trình 3( x+2/x-1)^2 + 25(x-2/x+1)^2 - 20( x^2-4/x^2-1) =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2021
3(2x+y)-2(3x-2y)=3.19-11.2
6x+3y-6x+4y=57-22
7y=35
y=5
thay vào :
2x+y=19
2x+5=19
2x=14
x=7
2/ x2+21x-1x-21=0
x(x+21)-1(x+21)=0
(x+21)(x-1)=0
TH1 x+21=0
x=-21
TH2 x-1=0
x=1
vậy x = {-21} ; {1}
3/ x4-16x2-4x2+64=0
x2(x2-16)-4(x2-16)=0
(x2-16)-(x2-4)=0
TH1 x2-16=0
x2=16
<=>x=4;-4
TH2 x2-4=0
x2=4
x=2;-2
18 tháng 5 2021
Bài 1 :
\(\hept{\begin{cases}2x+y=19\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}4x+2y=38\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}7x=49\\2x+y=19\end{cases}}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=7\\2x+y=19\end{cases}}\)Thay vào x = 7 vào pt 2 ta được :
\(14+y=19\Leftrightarrow y=5\)Vậy hệ pt có một nghiệm ( x ; y ) = ( 7 ; 5 )
Bài 2 :
\(x^2+20x-21=0\)
\(\Delta=400-4\left(-21\right)=400+84=484\)
\(x_1=\frac{-20-22}{2}=-24;x_2=\frac{-20+22}{2}=1\)
Bài 3 : Đặt \(x^2=t\left(t\ge0\right)\)
\(t^2-20t+64=0\)
\(\Delta=400+4.64=656\)
\(t_1=\frac{20+4\sqrt{41}}{2}\left(tm\right);t_2=\frac{20-4\sqrt{41}}{2}\left(ktm\right)\)
Theo cách đặt : \(x^2=\frac{20+4\sqrt{41}}{2}\Rightarrow x=\sqrt{\frac{20+4\sqrt{41}}{2}}=\frac{\sqrt{20\sqrt{2}+4\sqrt{82}}}{2}\)
HH
8 tháng 7 2018
1/ \(1+\frac{2}{x-1}+\frac{1}{x+3}=\frac{x^2+2x-7}{x^2+2x-3}\)
ĐKXĐ: \(\hept{\begin{cases}x-1\ne0\\x+3\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne1\\x\ne-3\end{cases}}\)
<=> \(1+\frac{2\left(x+3\right)+x-1}{\left(x-1\right)\left(x+3\right)}=\frac{x^2+2x-3-5}{x^2+2x-3}\)
<=> \(1+\frac{2x+6+x-1}{x^2+2x-3}=1-\frac{5}{x^2+2x-3}\)
<=> \(\frac{3x+5}{x^2+2x-3}+\frac{5}{x^2+2x-3}=1-1\)
<=> \(\frac{3x+5}{x^2+2x-3}+\frac{5}{x^2+2x-3}=0\)
<=> \(\frac{3x+10}{x^2+2x-3}=0\)
<=> \(3x+10=0\)
<=> \(x=-\frac{10}{3}\)
25 tháng 2 2022
a,\(\left(x-4-5\right)\left(x-4+5\right)=0\Leftrightarrow\left(x-9\right)\left(x+1\right)=0\Leftrightarrow x=9;x=-1\)
b, \(\left(x-3-x-1\right)\left(x-3+x+1\right)=0\Leftrightarrow2x-2=0\Leftrightarrow x=1\)
c, \(\left(x^2-4\right)\left(2x-3\right)-\left(x^2-4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(2x-3-x+1\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x-2\right)=0\Leftrightarrow x=-2;x=2\)
d, \(\left(3x-7\right)^2-\left(2x+2\right)^2=0\Leftrightarrow\left(3x-7-2x-2\right)\left(3x-7+2x+2\right)=0\)
\(\Leftrightarrow\left(x-9\right)\left(5x-5\right)=0\Leftrightarrow x=1;x=9\)
VD
18 tháng 3 2022
\(a,4+3x=25-4x\\ \Leftrightarrow7x=21\\ \Leftrightarrow x=3\\ b,\left(x-1\right)^2+\left(x-1\right)\left(x+3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-1+x+3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(2x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
c, ĐKXĐ:\(x\ne-1,x\ne2\)
\(\dfrac{1}{x+1}+\dfrac{3}{x-2}=\dfrac{9}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow\dfrac{x-2}{\left(x+1\right)\left(x-2\right)}+\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}-\dfrac{9}{\left(x+1\right)\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x-2+3x+3-9}{\left(x+1\right)\left(x-2\right)}=0\\ \Rightarrow4x-8=0\\ \Leftrightarrow x=2\left(ktm\right)\)
VD
18 tháng 3 2022
\(a,2x-5=-x+4\\ \Leftrightarrow3x=9\\ \Leftrightarrow x=3\\ b,\left(4x-10\right)\left(25+5x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x-10=0\\25+5x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-5\end{matrix}\right.\\ c,\dfrac{x}{3}-\dfrac{2x+1}{2}=\dfrac{x}{6}-x\\ \Leftrightarrow\dfrac{2x}{6}-\dfrac{3\left(2x+1\right)}{6}-\dfrac{x}{6}+\dfrac{6x}{6}=0\\ \Leftrightarrow2x-6x-3-x+6x=0\\ \Leftrightarrow x-3=0\\ \Leftrightarrow x=3\)
d, ĐKXĐ:\(x\ne-2,x\ne3\)
\(1+\dfrac{x}{3-x}=\dfrac{5x}{\left(x+2\right)\left(3-x\right)}+\dfrac{2}{x+2}\\ \Leftrightarrow\dfrac{\left(x+2\right)\left(3-x\right)}{\left(x+2\right)\left(3-x\right)}+\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(3-x\right)}-\dfrac{5x}{\left(x+2\right)\left(3-x\right)}-\dfrac{2\left(3-x\right)}{\left(x+2\right)\left(3-x\right)}=0\\ \Leftrightarrow\dfrac{-x^2+x+6}{\left(x+2\right)\left(3-x\right)}+\dfrac{x^2+2x}{\left(x+2\right)\left(3-x\right)}-\dfrac{5x}{\left(x+2\right)\left(3-x\right)}-\dfrac{6-2x}{\left(x+2\right)\left(3-x\right)}=0\)
\(\Leftrightarrow\dfrac{-x^2+x+6+x^2+2x-5x-6+2x}{\left(x+2\right)\left(3-x\right)}=0\\ \Rightarrow0=0\left(luôn.đúng\right)\)
1 tháng 2 2021
cấy pt dạng ni lớp 8 học rồi mà :v
chỉ là thêm công thức nghiệm vào thôi ._.
1. ( x + 2 )( x + 4 )( x + 6 )( x + 8 ) + 16 = 0
<=> [ ( x + 2 )( x + 8 ) ][ ( x + 4 )( x + 6 ) ] + 16 = 0
<=> ( x2 + 10x + 16 )( x2 + 10x + 24 ) + 16 = 0
Đặt t = x2 + 10x + 16
pt <=> t( t + 8 ) + 16 = 0
<=> t2 + 8t + 16 = 0
<=> ( t + 4 )2 = 0
<=> ( x2 + 10x + 16 + 4 )2 = 0
<=> ( x2 + 10x + 20 )2 = 0
=> x2 + 10x + 20 = 0
Δ' = b'2 - ac = 25 - 20 = 5
Δ' > 0 nên phương trình có hai nghiệm phân biệt
\(x_1=\frac{-b'+\sqrt{\text{Δ}'}}{a}=-5+\sqrt{5}\)
\(x_2=\frac{-b'-\sqrt{\text{Δ}'}}{a}=-5-\sqrt{5}\)
Vậy ...
2. ( x + 1 )( x + 2 )( x + 3 )( x + 4 ) - 24 = 0
<=> [ ( x + 1 )( x + 4 ) ][ ( x + 2 )( x + 3 ) ] - 24 = 0
<=> ( x2 + 5x + 4 )( x2 + 5x + 6 ) - 24 = 0
Đặt t = x2 + 5x + 4
pt <=> t( t + 2 ) - 24 = 0
<=> t2 + 2t - 24 = 0
<=> ( t - 4 )( t + 6 ) = 0
<=> ( x2 + 5x + 4 - 4 )( x2 + 5x + 4 + 6 ) = 0
<=> x( x + 5 )( x2 + 5x + 10 ) = 0
Vì x2 + 5x + 10 có Δ = -15 < 0 nên vô nghiệm
=> x = 0 hoặc x = -5
Vậy ...
3. ( x - 1 )( x - 3 )( x - 5 )( x - 7 ) - 20 = 0
<=> [ ( x - 1 )( x - 7 ) ][ ( x - 3 )( x - 5 ) ] - 20 = 0
<=> ( x2 - 8x + 7 )( x2 - 8x + 15 ) - 20 = 0
Đặt t = x2 - 8x + 7
pt <=> t( t + 8 ) - 20 = 0
<=> t2 + 8t - 20 = 0
<=> ( t - 2 )( t + 10 ) = 0
<=> ( x2 - 8x + 7 - 2 )( x2 - 7x + 8 + 10 ) = 0
<=> ( x2 - 8x + 5 )( x2 - 7x + 18 ) = 0
<=> \(\orbr{\begin{cases}x^2-8x+5=0\\x^2-7x+18=0\end{cases}}\)
+) x2 - 8x + 5 = 0
Δ' = b'2 - ac = 16 - 5 = 11
Δ' > 0 nên có hai nghiệm phân biệt
\(x_1=\frac{-b'+\sqrt{\text{Δ}'}}{a}=-4+\sqrt{11}\)
\(x_2=\frac{-b'+\sqrt{\text{Δ}'}}{a}=-4-\sqrt{11}\)
+) x2 - 7x + 18 = 0
Δ = b2 - 4ac = 49 - 72 = -23 < 0 => vô nghiệm
Vậy ...
23 tháng 2 2023
a: =>(2x-5x-1)(2x+5x+1)=0
=>(-3x-1)(7x+1)=0
=>x=-1/3 hoặc x=-1/7
b: =>(5x-5)^2-(x+2)^2=0
=>(5x-5-x-2)(5x-5+x+2)=0
=>(4x-7)(6x-3)=0
=>x=1/2 hoặc x=7/4
c: =>(x^2+4x-1-x^2+3x-2)(x^2+4x-1+x^2-3x+2)=0
=>(7x-3)(2x^2+x+1)=0
=>7x-3=0
=>x=3/7
5 tháng 2 2016
<=> 20(x - 2)/(x - 1) - 5(x + 2)²/(x- 1)² + 48(x² - 4) / (x-1)(x+1) = 0
Điều kiện :
{ x- 1 # 0
{ x+1 # 0
{ x # 1
{ x # -1
=> 20(x-2)(x+1)(x-1) - 5(x+2)²(x + 1) + 48(x² - 4)(x - 1) = 0
<=> 20(x-2)(x² - 1) - 5(x² + 4x+4)(x + 1) + 48(x^3 - x² - 4x + 4) = 0
<=> 20(x^3 - x - 2x² + 2) - 5(x^3 + x² + 4x² + 4x + 4x + 4 ) + 48(x^3 - x² - 4x + 4) = 0
<=> 20(x^3 - x - 2x² + 2) - 5(x^3 + 5x² + 8x + 4 ) + 48(x^3 - x² - 4x + 4) = 0
<=> 20x^3 - 20x - 40x² + 40 - 5x^3 - 25x² - 40x - 20 + 48x^3 - 48x² - 192x + 192 = 0
<=> 63x^3 - 113x² - 252x + 212 = 0
Ta có
Δ = b² - 3ac = (-113)² - 3.63.(-252) = 60397
k = 9abc - 2b^3 - 27a²d / 2√|Δ|^3 = -0,1241
Vì Δ > 0 và |k| < 1 nên pt có 3 nghiệm
x = 2√Δ.cos(arccos(k)/3 ) - b / 3a = 2,794
x = 2√Δ.cos(arccos(k) + 2r/3 ) - b / 3a = -1,706
x = 2√Δ.cos(arccos(k) - 2r/3 ) - b / 3a = 0,706
nha
5 tháng 2 2016
Nguyễn Vũ Dũng mấy cái kí hiệu ở cuối là sao bạn?
5 tháng 2 2016
<=> 20(x - 2)/(x - 1) - 5(x + 2)²/(x- 1)² + 48(x² - 4) / (x-1)(x+1) = 0
Điều kiện :
{ x- 1 # 0
{ x+1 # 0
{ x # 1
{ x # -1
=> 20(x-2)(x+1)(x-1) - 5(x+2)²(x + 1) + 48(x² - 4)(x - 1) = 0
<=> 20(x-2)(x² - 1) - 5(x² + 4x+4)(x + 1) + 48(x^3 - x² - 4x + 4) = 0
<=> 20(x^3 - x - 2x² + 2) - 5(x^3 + x² + 4x² + 4x + 4x + 4 ) + 48(x^3 - x² - 4x + 4) = 0
<=> 20(x^3 - x - 2x² + 2) - 5(x^3 + 5x² + 8x + 4 ) + 48(x^3 - x² - 4x + 4) = 0
<=> 20x^3 - 20x - 40x² + 40 - 5x^3 - 25x² - 40x - 20 + 48x^3 - 48x² - 192x + 192 = 0
<=> 63x^3 - 113x² - 252x + 212 = 0
Ta có
Δ = b² - 3ac = (-113)² - 3.63.(-252) = 60397
k = 9abc - 2b^3 - 27a²d / 2√|Δ|^3 = -0,1241
Vì Δ > 0 và |k| < 1 nên pt có 3 nghiệm
x = 2√Δ.cos(arccos(k)/3 ) - b / 3a = 2,794
x = 2√Δ.cos(arccos(k) + 2r/3 ) - b / 3a = -1,706
x = 2√Δ.cos(arccos(k) - 2r/3 ) - b / 3a = 0,706
5 tháng 2 2016
c) 20(x - 2)/(x - 1) - 5(x + 2)²/(x- 1)² + 48(x² - 4)/(x² - 1) = 0
<=> 20(x - 2)/(x - 1) - 5(x + 2)²/(x- 1)² + 48(x² - 4) / (x-1)(x+1) = 0
Điều kiện :
{ x- 1 # 0
{ x+1 # 0
{ x # 1
{ x # -1
=> 20(x-2)(x+1)(x-1) - 5(x+2)²(x + 1) + 48(x² - 4)(x - 1) = 0
<=> 20(x-2)(x² - 1) - 5(x² + 4x+4)(x + 1) + 48(x^3 - x² - 4x + 4) = 0
<=> 20(x^3 - x - 2x² + 2) - 5(x^3 + x² + 4x² + 4x + 4x + 4 ) + 48(x^3 - x² - 4x + 4) = 0
<=> 20(x^3 - x - 2x² + 2) - 5(x^3 + 5x² + 8x + 4 ) + 48(x^3 - x² - 4x + 4) = 0
<=> 20x^3 - 20x - 40x² + 40 - 5x^3 - 25x² - 40x - 20 + 48x^3 - 48x² - 192x + 192 = 0
<=> 63x^3 - 113x² - 252x + 212 = 0
Ta có
Δ = b² - 3ac = (-113)² - 3.63.(-252) = 60397
k = 9abc - 2b^3 - 27a²d / 2√|Δ|^3 = -0,1241
Vì Δ > 0 và |k| < 1 nên pt có 3 nghiệm
x = 2√Δ.cos(arccos(k)/3 ) - b / 3a = 2,794
x = 2√Δ.cos(arccos(k) + 2r/3 ) - b / 3a = -1,706
x = 2√Δ.cos(arccos(k) - 2r/3 ) - b / 3a = 0,706