Chứng minh rằng đường thẳng luôn cắt đường tròn
tại hai điểm phân biệt A, B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
3 tháng 3 2021
Lời giải:
a) Ta có:
$\widehat{MAK}=\widehat{ACE}$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nt chắn cung đó)
$AC\parallel MB$ nên $\widehat{ACE}=\widehat{EMK}$ (so le trong)
$\Rightarrow \widehat{MAK}=\widehat{EMK}$
Xét tam giác $MAK$ và $EMK$ có:
$\widehat{MAK}=\widehat{EMK}$ (cmt)
$\widehat{K}$ chung
$\Rightarrow \triangle MAK\sim \triangle EMK$ (g.g)
$\Rightarrow \frac{MK}{AK}=\frac{EK}{MK}\Rightarrow MK^2=AK.EK$
b)
Hoàn toàn tương tự, dễ thấy $\triangle KEB\sim \triangle KBA$ (g.g)
$\Rightarrow \frac{KE}{KB}=\frac{KB}{KA}\Rightarrow KB^2=AK.EK$
Kết hợp với phần 1) suy ra $KB^2=MK^2\Rightarrow KB=MK$ (đpcm)
21 tháng 2 2023
1: Điểm cố định của (d) là:
x=0 và y=m*0+2=2
2: PTHĐGĐ là:
x2-mx-2=0
a=1; b=-m; c=-2
Vì a*c<0
nên (P) luôn cắt (d) tại hai điểm khác phía so với trục tung
4 tháng 4 2022
b: Phương trình hoành độ giao điểm là:
\(x^2+\left(m-2\right)x-m^2-1=0\)
\(ac=-m^2-1< 0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt
27 tháng 5 2023
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>AC/AD=MA/MD
=>MA*AD=AC*MD
CM
2 tháng 11 2018
Phương trình hoành độ giao điểm của (C) và đường thẳng (d) y = 2x + m là:
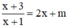
⇔ (2x + m)(x + 1) = x + 3
Vậy với mọi m ∈ R, (d) cắt (C) tại hai điểm phân biệt MN.
31 tháng 3 2016
a) MNAC nội tiếp MA.MD=MB.MC phương tích
b) ˆNCA=ˆNBA⇒NA.NB=NH.NONCA^=NBA^⇒NA.NB=NH.NO
c) ý bạn là đường thẳng nào
nó cũng có thể giao tại 1 điểm hoặc ko giao mà bạn