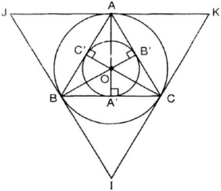
Cho tam giác ABC ngoại tiếp (O;R). (O;R) tiếp xúc với các cạnh BC,AB thứ tự tại D,N. Kẻ đường kính DI của (O). Tiếp tuyến của (O) tại I cắt các cạnh AB,AC thứ tự tại E và F.
1) C/m tứ giác OIEN nội tiếp đường tròn
2)C/m tam giác BOE vuông và EI.BD = FI.CD = \(R^2\)
3) Gọi \(A_1\) là giao điểm của AO với cạnh BC, \(B_1\) là giap điểm của BO với cạnh AC, \(C_1\) là giao điểm của CO với cạnh AB. Chứng minh : \(\frac{AO}{AA_1}+\frac{BO}{BB_1}+\frac{CO}{CC_1}=2\)

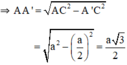
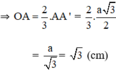
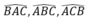

@Nguyễn Việt Lâm please help meeeeeeeee!!!!!!!!!!!!~~