xác định tính liên tục của hàm số trên r
f(x)=2sinx+3tan2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2018
Xét tính liên tục của hàm số sau trên tập xác định của nó:
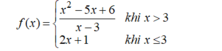
● Hàm số liên tục với mọi x ≠ 3.
● Tại x = 3, ta có:
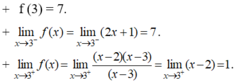
⇒ Hàm số không liên tục tại x = 3.
- Vậy hàm số liên tục trên các khoảng (-∞ ; 3), (3 ; +∞).
CM
25 tháng 3 2017
Đáp án C
Ta có y ' = f ' x − 2 dựa trên đồ thị ta thấy x ∈ 1 ; + ∞ ⇒ f ' x > 2 ⇒ f ' x − 2 > 0 ⇒ y đồng biến
CM
6 tháng 2 2018
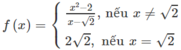
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì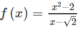 
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
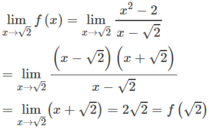
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
CM
1 tháng 7 2017
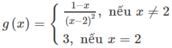
có tập xác định là D = R
- Nếu x ≠ 2 thì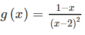 
là hàm phân thức hữu tỉ, nên nó liên tục trên các khoảng (-∞; 2) và (2; +∞)
Tại x = 2: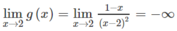 
Vậy hàm số y = g(x) không liên tục tại x = 2
Kết luận: y = g(x) liên tục trên các khoảng (-∞; 2) và (2; +∞) nhưng gián đoạn tại x = 2
CM
22 tháng 7 2018
a) Đồ thị hàm số (hình bên).
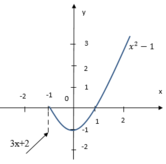
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
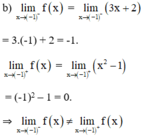
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
14 tháng 7 2023
a: TXĐ: D=R
x^2;sin x đều liên tục trên R
=>f(x) liên tục trên R
b: TXĐ: D=R\{1}
x^4;-x^2;6/x-1 đều liên tục khi x thuộc (-vô cực;1) hoặc (1;+vô cực)
=>g(x) liên tục trên (-vô cực;1) và (1;+vô cực)
c: ĐKXĐ: x<>3; x<>-4
HS \(\dfrac{2x}{x-3}\) liên tục trên (-vô cực;3) và (3;+vô cực)
(x-1)/(x+4) liên tục trên (-vô cực;-4) và (-4;+vô cực)
=>h(x) liên tục trên từng khoảng xác định của nó
Mục tiêu -500 sp mong giúp đỡ