Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 
Phương trình đường cao AH đi qua A(2;-1) nhận 
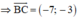
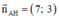là VTPT là: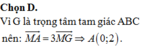
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
A B → = 3 ; 12 , A C → = 4 ; − 1 ⇒ ( A B ) ⃗ . ( A C ) ⃗ = 3 . 4 + 12 . ( - 1 ) = 0 ⇒ ∆ A B C vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B
1/ Hướng làm như sau:
- Ta sẽ viết phương trình đường thẳng của 2 cạnh AB và AC trước
- Lấy một điểm bất kỳ thuộc đường phân giác trong của góc A. Vì điểm nằm trên đường phân giác cách đều 2 tia tạo thành góc đó nên ta sẽ tính khoảng cách giữa điểm đó với 2 cạnh của tam giác rồi cho chúng bằng nhau
\(\overrightarrow{AB}=\left(1-\frac{7}{4};2-3\right)=\left(-\frac{3}{4};-1\right)\Rightarrow AB:\left(x-1\right)-\frac{3}{4}\left(y-2\right)=0\)
\(\Rightarrow AB:x-\frac{3}{4}y+\frac{1}{2}=0\)
\(\overrightarrow{AC}=\left(-4-\frac{7}{4};3-3\right)=\left(-\frac{23}{4};0\right)\) \(\Rightarrow AC:\frac{23}{4}\left(y-3\right)=0\Rightarrow AC:\frac{23}{4}y-\frac{69}{4}=0\)
Gọi \(M\left(x;y\right)\) là điểm thuộc đường phân giác góc A và nằm trên BC
\(\Rightarrow d\left(M;AB\right)=\frac{\left|1.x_M-\frac{3}{4}y_M+\frac{1}{2}\right|}{\sqrt{1+\frac{9}{16}}}=...\)
\(\Rightarrow d\left(M;AC\right)=\frac{\left|0.x_M+\frac{23}{4}.y_M-\frac{69}{4}\right|}{\sqrt{0+\left(\frac{23}{4}\right)^2}}=...\)
\(d\left(M;AB\right)=d\left(M;AC\right)\Leftrightarrow\frac{\left|x_M-\frac{3}{4}y_M+\frac{1}{2}\right|}{\frac{5}{4}}=\frac{\left|\frac{23}{4}y_M-\frac{69}{4}\right|}{\frac{23}{4}}\)
\(\Leftrightarrow\left[{}\begin{matrix}23\left(x_M-\frac{3}{4}y_M+\frac{1}{2}\right)=5\left(\frac{23}{4}y_M-\frac{69}{4}\right)\\23\left(x_M-\frac{3}{4}y_M+\frac{1}{2}\right)=5\left(\frac{69}{4}-\frac{23}{4}y_M\right)\end{matrix}\right.\)
Đến đây ta thấy vẫn còn 2 ẩn là xM và yM. Mà \(M\in BC\) nên ta sẽ sử dụng phương trình đường thẳng BC để đưa về một ẩn
\(\overrightarrow{BC}=\left(-4-1;3-2\right)=\left(-5;1\right)\) \(\Rightarrow BC:-5\left(x-1\right)+\left(y-2\right)=0\)
\(\Rightarrow BC:-5x+y+3=0\) \(\Rightarrow y_M=5x_M-3\)
Đến đây thay vô là được thôi bạn :) Có 2 trường hợp đó, một cái là điểm M nằm trong, dành cho phân giác trong và ngược lại.
Và làm thế nào để biết được đâu là trong đâu là ngoài? Đơn giản thôi, ta thấy điểm M thuộc BC, sẽ có \(\overrightarrow{BM}=x\overrightarrow{MC}\)
Nếu x>0 nghĩa là M nằm trên đoạn BC còn nếu <0 nghĩa là nằm ngoài BC. Câu 2 tương tự nhé :3
P/s: Tính toán lại hộ mình nhé :<< Nhiều số quá rối hết cả mắt :<<
Câu 1 có 1 cách giải đơn giản ngắn gọn:
- Tính vecto \(\overrightarrow{BC}\) ; \(\overrightarrow{AB};\overrightarrow{AC}\Rightarrow\) độ dài AB;AC;BC
- Gọi D là chân đường phân giác trong của A trên BC
- Theo định lý phân giác: \(\frac{DB}{AB}=\frac{DC}{AC}\Rightarrow\) tỉ lệ \(\frac{BD}{DC}\)
\(\Rightarrow\) Tọa độ D (điểm chia đoạn thẳng theo tỉ số k)
\(\Rightarrow\) Phương trình AD
Câu 2
Làm tương tự, sau khi tìm được tọa độ chân đường phân giác trong \(\Rightarrow\) tính được vecto \(\overrightarrow{AD}\)
Do 2 đường phân giác trong và ngoài vuông góc nên đường phân giác ngoài nhận \(\overrightarrow{AD}\) là 1 vtpt. Vậy là viết được pt phân giác ngoài