cho x,y là hai số dương thỏa mãn x2+y2=1. Tìm GTLN của P=xy+3x+3y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2023
Ta có \(x^2+y^2=1\Leftrightarrow\left(x+y\right)^2=2xy+1\)
Từ đó \(P=\dfrac{\left(x+y\right)^2}{x+y+1}\). Đặt \(x+y=t\left(t\ge0\right)\). Vì \(x+y\le\sqrt{2\left(x^2+y^2\right)}=2\) nên \(t\le\sqrt{2}\). ĐTXR \(\Leftrightarrow x=y=\dfrac{1}{\sqrt{2}}\). Ta cần tìm GTLN của \(P\left(t\right)=\dfrac{t^2}{t+1}\) với \(0\le t\le\sqrt{2}\).
Giả sử có \(0\le t_1\le t_2\le\sqrt{2}\). Ta có BDT luôn đúng \(\left(t_2-t_1\right)\left(t_2+t_1+t_2t_1\right)\ge0\) \(\Leftrightarrow t_2^2-t_1^2+t_2^2t_1-t_2t_1^2\ge0\) \(\Leftrightarrow t_1^2\left(t_2+1\right)\le t_2^2\left(t_1+1\right)\) \(\Leftrightarrow\dfrac{t_1^2}{t_1+1}\le\dfrac{t_2^2}{t_2+1}\) \(\Leftrightarrow P\left(t_1\right)\le P\left(t_2\right)\). Như vậy với \(0\le t_1\le t_2\le\sqrt{2}\) thì \(P\left(t_1\right)\le P\left(t_2\right)\). Do đó P là hàm đồng biến. Vậy GTLN của P đạt được khi \(t=\sqrt{2}\) hay \(x=y=\dfrac{1}{\sqrt{2}}\), khi đó \(P=2\sqrt{2}-2\)
AH
Akai Haruma
Giáo viên
30 tháng 4 2023
Lời giải:
$P=\frac{2xy+1}{x+y+1}=\frac{2xy+x^2+y^2}{x+y+1}=\frac{(x+y)^2}{x+y+1}$
$=\frac{a^2}{a+1}$ với $x+y=a$
Áp dụng BĐT AM-GM:
$1=x^2+y^2\geq \frac{(x+y)^2}{2}=\frac{a^2}{2}$
$\Rightarrow a^2\leq 2\Rightarrow a\leq \sqrt{2}$
$P=\frac{a^2}{a+1}=\frac{a}{1+\frac{1}{a}}$
Vì $a\leq \sqrt{2}\Rightarrow 1+\frac{1}{a}\geq 1+\frac{1}{\sqrt{2}}=\frac{2+\sqrt{2}}{2}$
$\Rightarrow P\leq \frac{\sqrt{2}}{\frac{2+\sqrt{2}}{2}}=-2+2\sqrt{2}$
Vậy $P_{\max}=-2+2\sqrt{2}$ khi $x=y=\frac{1}{\sqrt{2}}$
HN
1
16 tháng 2 2020
\(10=4x^2+4y^2+6=\left(x^2+y^2\right)+3\left(x^2+1\right)+3\left(y^2+1\right)\)
\(2xy+6x+6y=2\left(xy+3x+3y\right)\Rightarrow P\le5\) tại \(x=y=\frac{1}{\sqrt{2}}\)
13 tháng 1 2021
Áp dụng bất đẳng thức AM - GM và kết hợp với giả thiết x + y + z = 3 ta có:
\(B=\sqrt{\dfrac{xy}{xy+z\left(x+y+z\right)}}+\sqrt{\dfrac{yz}{yz+x\left(x+y+z\right)}}+\sqrt{\dfrac{zx}{zx+y\left(x+y+z\right)}}\)
\(B=\sqrt{\dfrac{xy}{\left(x+z\right)\left(y+z\right)}}+\sqrt{\dfrac{yz}{\left(y+x\right)\left(z+x\right)}}+\sqrt{\dfrac{zx}{\left(z+y\right)\left(z+x\right)}}\le\dfrac{1}{2}\left(\dfrac{x}{x+z}+\dfrac{y}{y+z}+\dfrac{y}{y+x}+\dfrac{z}{z+x}+\dfrac{z}{z+y}+\dfrac{x}{z+x}\right)\)
\(B\le\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = z = 1.
Vậy...
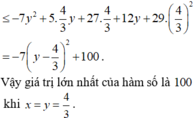
Ta có \(x+y\le\sqrt{2\left(x^2+y^2\right)}\)(bđt Bunhiacopski)
Áp dụng bđt AM-GM ta có
\(P\le\frac{x^2+y^2}{2}+3.\sqrt{2\left(x^2+y^2\right)}\)\(=\frac{1}{2}+3\sqrt{2}=\frac{1+6\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(x=y=\frac{\sqrt{2}}{2}\)
Vậy............
thank you