Tính diện tích cạnh của hình tám cạnh đều theo bán kính R của đường tròn ngoại tiếp hình đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 4 2017
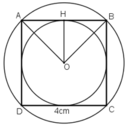
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
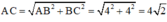(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
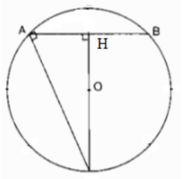
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
CM
19 tháng 6 2017
Đáp án B
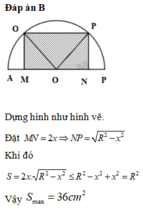
Dựng hình như hình vẽ. Đặt M N = 2 x ⇒ N P = R 2 − x 2
Khi đó S = 2 x . R 2 − x 2 ≤ R 2 − x 2 + x 2 = R 2
Vậy S max = 36 c m 2
30 tháng 5 2021
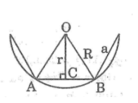
-từ S hình vuông => cạnh tam giác =4
- BK= \(R=\frac{1}{2}.\frac{4}{\cos30}=\frac{4}{\sqrt{3}}\left(cm\right)\)
13 tháng 4 2017
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
Hướng dẫn trả lời:
a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:
- Vẽ AB = 4cm.
- Vẽ BC ⊥ AB và BC = 4cm
- Vẽ DC ⊥ BC và DC = 4cm
- Nối D với A, ta có AD ⊥ DC và AD = 4cm
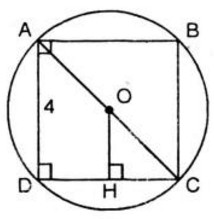
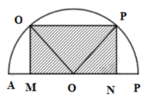
b) Tam giác ABC là tam giác vuông cân nên AB = BC.
Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:
AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=√32=4√2AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=32=42
Vậy AO=R=AC2=4√22=2√2AO=R=AC2=422=22
Vậy R = 2√2 cm
c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD
Ta có: OH=AD2=2(cm)OH=AD2=2(cm)
Vậy r = OH = 2cm
\
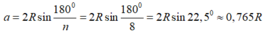
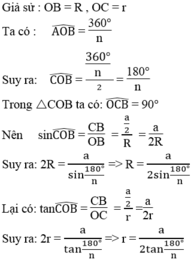
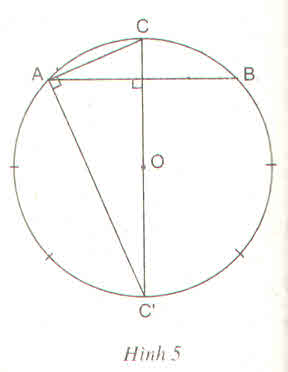
Giả sử AB là 1 cạnh của hình tám cạnh đều, gọi AB=a.
Vẽ AK là đường co của tam giác OAB
Ta có: \(\widehat{AOB}=\frac{360^o}{8}=45^o\Rightarrow OK=AK=\sin45^o=\frac{OA\sqrt{2}}{2}=\frac{R\sqrt{2}}{2}\)
Nên KB=OB-OK=\(\frac{R\sqrt{2}}{2}-R=R\left(\frac{\sqrt{2}}{2}-1\right)\)
Xét tam giác KAB vuông tại K, theo định lý Pytago ta có:
\(AB^2=AK^2+KB^2=\left(\frac{R\sqrt{2}}{2}\right)^2+\left[R\left(\frac{\sqrt{2}}{2}-1\right)\right]^2\)
\(AB^2=R^2\left(\frac{1}{2}+\frac{1}{2}-\sqrt{2}+1\right)\)
\(\Rightarrow AB^2=\left(2-\sqrt{2}\right)R^2\)
\(\Rightarrow AB=\sqrt{2-\sqrt{2}}R\)