Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm M của mỗi đường (AB # CD)
a' Chứng minh AC=BD
b'Chứng minh AD=BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo https://h.vn/hoi-dap/question/147625.html nha

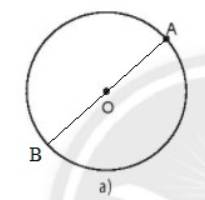
a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
b) Độ dài IM = IM'.

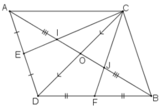
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB

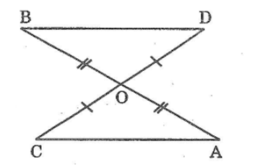
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
CM
a) Vì M là trung điểm của đoạn thẳng AB nên
=> AM = BM ( tính chất trung điểm của đoạn thẳng )
Vì M là trung điểm của CD nên
=> CM = DM ( tính chất trung điểm của đoạn thẳng )
Xét tam giác AMC và tam giác BMD ta có:
AM =BM (CM trên)
CM = DM (CM trên)
góc AMC = góc BMD ( 2 góc đối đỉnh)
=> Tam giác AMC = tam giác BMD ( c.g.c)
=> AC = BD ( 2 cạnh tương ứng )
b) Xét tam giác AMD và tam giác BMC ta có:
AM = BM (CM phần a)
DM=CM (CM phần a)
góc AMD = góc CMB (2 góc đối đỉnh)
=> tam giác AMD = tam giác BMC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
Học tốt. Nhớ k cho mik nha.