Hình vuông có đường chéo bằng 6 thì cạnh hình vuông bằng :
A. ;B. 9 ;C. 18 ;D. 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 7 2017
a)
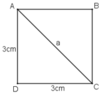
Gọi đường chéo của hình vuông có độ dài là a.
Áp dụng định lí Pi-ta-go ta có:
a2 = 32 + 32 = 18 suy ra a = √18 = 3√2
Vậy đường chéo của hình vuông đó bằng 3√2 (cm)
b)
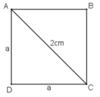
Gọi cạnh của hình vuông là a.
Áp dụng định lí Pi-ta-go ta có:
a2 + a2 = 22 ⇒ 2a2 = 4
⇒ a2 = 2 ⇒ a = √2
Vậy cạnh của hình vuông đó bằng √2 (dm).
18 tháng 10 2023
Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)
Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.
Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\)
\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\)
(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))
Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).
Vậy \(a=2\) thỏa mãn ycbt.
26 tháng 12 2021
a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 3 2023
Diện tích của hình vuông: \(5\times5=25\left(dm^2\right)\)
Chiều dài đường chéo còn lại: \(25\times2:5=10\left(dm\right)\)
1 tháng 12 2023
a: ABCD là hình vuông
=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC
AC là phân giác của góc DAB
=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)
AEBF là hình vuông
=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\)
=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)
\(\widehat{BAE}=45^0\)
\(\widehat{BAC}=45^0\)
Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)
=>AE và AC là hai tia trùng nhau
=>A,E,C thẳng hàng
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
AEBF là hình vuông
=>BA là phân giác của góc EBF
=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)
=>\(\widehat{ABE}=\widehat{ABD}\)
=>BE,BD là hai tia trùng nhau
=>B,E,D thẳng hàng
B,E,D thẳng hàng
A,E,C thẳng hàng
Do đó: BD cắt AC tại E
ADCB là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB
E là trung điểm của AC nên AC=2AE=2(cm)
E là trung điểm của BD nên BD=2EB=2(cm)
Xét tứ giác ADCB có DB\(\perp\)AC
nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)
b: ADCB là hình vuông
=>\(S_{ADCB}=AB^2\)
=>\(AB^2=2\)
=>\(AB=\sqrt{2}\left(cm\right)\)
CM
16 tháng 2 2019
Hình vuông có độ dài cạnh là a( cm )
Áp dụng định lý Py – to – go thì độ dài đường chéo của hình vuông là a 2 ( c m )
Do đó với a = 4 thì độ dài đường chéo là 4 2 = 32 ( c m )
Chọn đáp án B.
CM
24 tháng 4 2017
Hình vuông có độ dài cạnh là a ( cm )
Áp dụng định lý Py – to – go thì độ dài đường chéo của hình vuông là a 2 ( cm )
Do đó với a = 4 thì độ dài đường chéo là 4 2 = 32 ( c m )
Chọn đáp án B.
NT
0
HL
2
Hình vuông có đường chéo bằng 6 thì cạnh hình vuông bằng :
A. ;B. 9 ;C. 18 ;D. 6
Hình vuông có đường chéo bằng 6 thì cạnh hình vuông bằng :
A. ;B. 9 ;C. 18 ;D. 6
Trả lời :
Hình vuông có đường chéo bằng 6 thì cạnh hình vuông bằng :
A. \(3\sqrt{2}\) ;B. 9 ;C. 18 ;D. 6
học tốt
câu a nha bạn