Tam giac đêu nội tiếp đường tròn bán kính R=4cm . Tinh diện tích
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tam giác ABC đều nên tâm đường tròn ngoại tiếp O trùng trọng tâm
Gọi AM là trung tuyến (kiêm đường cao), theo tính chất trọng tâm:
\(AM=\dfrac{3}{2}AO=\dfrac{3}{2}R=12\)
\(AM=\dfrac{AB\sqrt{3}}{2}\Rightarrow AB=8\sqrt{3}\)
\(S=\dfrac{1}{2}AM.AB=48\sqrt{3}\)
Tam giác ABC đều.
\(\Rightarrow AB=AC=BC\) (Tính chất tam giác đều).
Áp dụng định lý sin vào tam giác ABC đều, ta có:
\(\dfrac{a}{\sin A}=2R.\Rightarrow\dfrac{BC}{\sin60}=2.8.\Leftrightarrow BC=16.\dfrac{\sqrt{3}}{2}=8\sqrt{3}\) (đvđd).
\(\Rightarrow BC^2=192\) (đvđd).
Ta có: \(S=\dfrac{1}{2}ac.\sin B.\)
\(\Rightarrow S=\dfrac{1}{2}BC.AB.\sin60^o=\dfrac{1}{2}.BC^2.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{4}.192=48\sqrt{3}\) (đvdt).

2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2

Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
=>\(\widehat{BOC}=75^0:\dfrac{1}{2}=150^0\)
Diện tích tam giác OBC là:
\(S_{OBC}=\dfrac{1}{2}\cdot OB\cdot OC\cdot sinBOC\)
\(=\dfrac{1}{2}\cdot1\cdot1\cdot sin150=\dfrac{1}{4}\)

Vẽ tam giác thường ABC nội tiếp đường tròn tâm O bán kính r
Ta có diện tích tam giác đều nội tiếp đường tròn (O;r) có S =r23√34r2334
Gọi I là trung điểm cung BC có chứa A
Dựng OI vuông góc BC tại H và cắt (O;r) tại K
Ta có Diện tích tam giác ABC < diện tích tam giác BIC
S BCI = IH.HB
S2BIC=HB2.IH2SBIC2=HB2.IH2
Lại có: BH2=HK.HIBH2=HK.HI (Hệ thức lượng)
Do đóS2BIC=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)SBIC2=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)
Áp dụng BĐT AM-GM ta có
HI+HI+HI+(6r−3HI)≥44√HI3.(6r−3IH)⇔32r≥44√HI3.(6r−3IH)HI+HI+HI+(6r−3HI)≥4HI3.(6r−3IH)4⇔32r≥4HI3.(6r−3IH)4
⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒3√34R2≥√IH3(2r−IH)=SBIC⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒334R2≥IH3(2r−IH)=SBIC
Do đóSABCSABC
Dấu "=" xảy ra khi HI = 6r -3IH
Do đó HI =32r32r
Vẽ tam giác thường ABC nội tiếp đường tròn tâm O bán kính r
Ta có diện tích tam giác đều nội tiếp đường tròn (O;r) có S =r23√34r2334
Gọi I là trung điểm cung BC có chứa A
Dựng OI vuông góc BC tại H và cắt (O;r) tại K
Ta có Diện tích tam giác ABC < diện tích tam giác BIC
S BCI = IH.HB
S2BIC=HB2.IH2SBIC2=HB2.IH2
Lại có: BH2=HK.HIBH2=HK.HI (Hệ thức lượng)
Do đóS2BIC=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)SBIC2=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)
Áp dụng BĐT AM-GM ta có
HI+HI+HI+(6r−3HI)≥44√HI3.(6r−3IH)⇔32r≥44√HI3.(6r−3IH)HI+HI+HI+(6r−3HI)≥4HI3.(6r−3IH)4⇔32r≥4HI3.(6r−3IH)4
⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒3√34R2≥√IH3(2r−IH)=SBIC⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒334R2≥IH3(2r−IH)=SBIC
Do đóSABCSABC
Dấu "=" xảy ra khi HI = 6r -3IH
Do đó HI =32r32r
Vẽ tam giác thường ABC nội tiếp đường tròn tâm O bán kính r
Ta có diện tích tam giác đều nội tiếp đường tròn (O;r) có S =r23√34r2334
Gọi I là trung điểm cung BC có chứa A
Dựng OI vuông góc BC tại H và cắt (O;r) tại K
Ta có Diện tích tam giác ABC < diện tích tam giác BIC
S BCI = IH.HB
S2BIC=HB2.IH2SBIC2=HB2.IH2
Lại có: BH2=HK.HIBH2=HK.HI (Hệ thức lượng)
Do đóS2BIC=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)SBIC2=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)
Áp dụng BĐT AM-GM ta có
HI+HI+HI+(6r−3HI)≥44√HI3.(6r−3IH)⇔32r≥44√HI3.(6r−3IH)HI+HI+HI+(6r−3HI)≥4HI3.(6r−3IH)4⇔32r≥4HI3.(6r−3IH)4
⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒3√34R2≥√IH3(2r−IH)=SBIC⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒334R2≥IH3(2r−IH)=SBIC
Do đóSABCSABC
Dấu "=" xảy ra khi HI = 6r -3IH
Do đó HI =32r32r
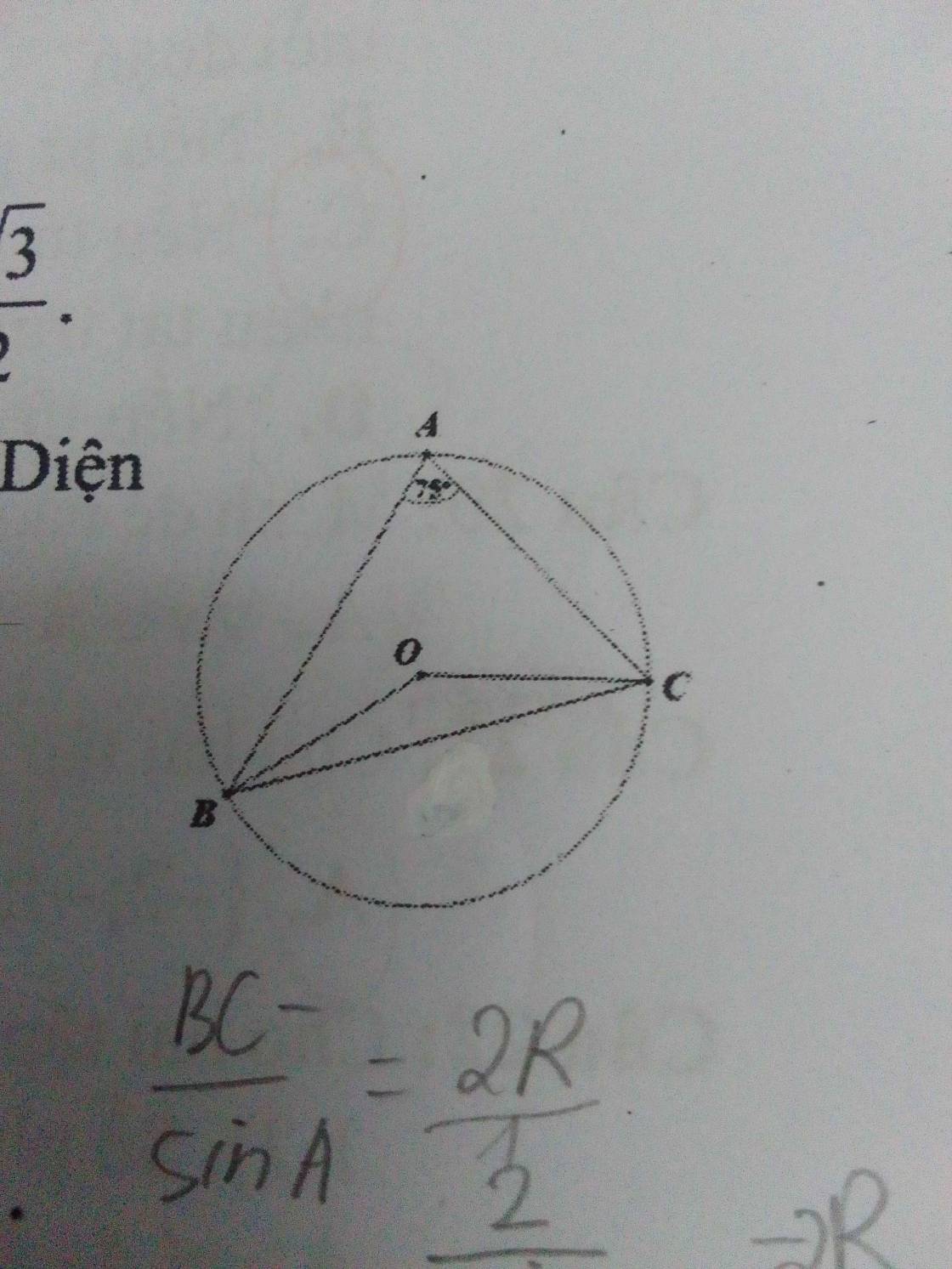
Xét \(\Delta\)ABC đều, có độ dài cạnh bằng a
Theo định lý sin ta có: \(\frac{BC}{\sin\widehat{BAC}}=2R\Leftrightarrow\frac{a}{\sin60^o}=2\cdot4\Leftrightarrow a=8\cdot\widehat{60^o}=4\sqrt{3}\)
Vậy diện tích tam giác cần tính là: \(S_{\Delta ABC}=\frac{1}{2}AB\cdot AC\cdot\sin\widehat{BAC}=\sin\left(4\sqrt{3}\right)^2\cdot\sin60^o=12\sqrt{3}\left(cm^2\right)\)
Nguồn: Hoàng Ngọc Khánh