Cho tam giác DEF vuông tại D, đường cao DI. Biết DF/EF=4/5 , DE = 18 cm . Giải tam giác DEF và tính độ dài...
Đọc tiếp
Cho tam giác DEF vuông tại D, đường cao DI. Biết DF/EF=4/5 , DE = 18 cm . Giải tam giác DEF và tính độ dài DI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2021
Bài 1:
\(CH=24\cdot\dfrac{3}{8}=9\left(cm\right)\)
DH=15(cm)
\(OH=3\sqrt{15}\left(cm\right)\)
\(OC=\sqrt{OH^2+CH^2}=\sqrt{81+135}=6\sqrt{6}\left(cm\right)\)
\(OD=\sqrt{24^2-216}=6\sqrt{10}\left(cm\right)\)
22 tháng 10 2021
Bài 1:
\(CH=24\cdot\dfrac{3}{8}=9\left(cm\right)\)
\(DH=15\left(cm\right)\)
\(OC=\sqrt{9\cdot24}=6\sqrt{6}\left(cm\right)\)
\(OD=\sqrt{24^2-216}=6\sqrt{10}\left(cm\right)\)
\(OH=3\sqrt{15}\left(cm\right)\)
H9
HT.Phong (9A5)
CTVHS
21 tháng 9 2023
a) Xét tam giác DEF vuông tại D có đường cao DI ta có:
\(\dfrac{1}{DI^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Rightarrow DI^2=\dfrac{DE^2DF^2}{DE^2+DF^2}\)
\(\Rightarrow DI^2=\dfrac{15^2\cdot20^2}{15^2+20^2}=144\)
\(\Rightarrow DI=12\left(cm\right)\)
b) Xét tam giác DEF vuông tại D có đường cao DI áp dụng Py-ta-go ta có:
\(DF^2=EF^2-DE^2\)
\(\Rightarrow DF^2=15^2-12^2=81\)
\(\Rightarrow DF=9\left(cm\right)\)
Ta có: \(DI=\sqrt{\dfrac{DF^2DE^2}{DF^2+DE^2}}\)
\(\Rightarrow DI=\sqrt{\dfrac{9^2\cdot12^2}{9^2+12^2}}=\dfrac{108}{15}\left(cm\right)\)
LM
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 9 2021
Áp dụng hệ thức lượng:
\(\dfrac{1}{DI^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Leftrightarrow DI=\dfrac{DE.DF}{\sqrt{DE^2+DF^2}}=\dfrac{3.4}{\sqrt{3^2+4^2}}=2,4\)
3 tháng 7 2021
- Áp dụng định lý pitago vào tam giác DEF vuông tại D :
\(DE=\sqrt{FE^2-DF^2}=27\left(cm\right)\)
- Áp dụng hệ thức lượng vào tam giác DEF vuông tại D đường cao DI
\(\left\{{}\begin{matrix}DI.FE=DE.DF\\DE^2=EI.FE\\DF^2=FI.FE\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}DI=21,6\\EI=16,2\\FI=28,8\end{matrix}\right.\) ( cm )
Vậy ...
3 tháng 7 2021
pyta go \(=>DE=\sqrt{ÈF^2-DF^2}=\sqrt{45^2-36^2}=27cm\)
áp dụng hệ thức lượng
\(=>DI.EF=DE.DF=>DI=\dfrac{27.36}{45}=21,6cm\)
\(=>DE^2=EI.EF=>EI=\dfrac{27^2}{45}=16,2cm\)
\(=>FI=45-16,2=28,8cm\)
10 tháng 5 2023
a: Xét ΔDKF vuông tại K và ΔEDF vuông tại D có
góc F chung
=>ΔDKF đồng dạng với ΔEDF
b: \(DF=\sqrt{20^2-16^2}=12\left(cm\right)\)
DK=12*16/20=9,6cm
c: MK/MD=FK/FD
DI/EI=FD/FE
mà FK/FD=FD/FE
nên MK/MD=DI/EI
CM
13 tháng 12 2017
I là trung điểm của EF nên IE = IF = EF/2 = 5cm.
Ta có :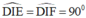 
⇒ ΔDIE vuông tại I
Theo định lý Pitago trong tam giác vuông DIE ta có :
DE2 = DI2 + EI2 ⇒ DI2 = DE2 – EI2 = 132 – 52 = 144 ⇒ DI = 12 (cm).
CM
9 tháng 3 2017
a, Ta có ∆DEF vuông vì D E 2 + D F 2 = F E 2
b, c, Tìm được: DK = 24 5 cm và HK = 32 5 cm
K D E ^ ≈ 36 0 52 ' ; K E D ^ = 35 0 8 '
d, Tìm được DM=3cm, FM=5cm và EM = 3 5 cm
e, f, Ta có: sin D F K ^ = D K D F ; sin D F E ^ = D E E F
=> D K D F = D E E F => ED.DF = DK.EF
\(\dfrac{DF}{EF}=\dfrac{4}{5}\)
\(\Leftrightarrow DF=\dfrac{4}{5}EF\)
\(\Leftrightarrow DF=24\left(cm\right)\)
\(\Leftrightarrow FE=30\left(cm\right)\)
\(\Leftrightarrow DI=14.4\left(cm\right)\)