Tam giác IKL vuông tại I. IH là đường cao kẻ từ I xuống KL. IH = ....(Nếu là phân số thì viết dưới dạng phân số tối giản)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 4 2023
a: Xét ΔMNP vuông tại M và ΔHIP vuông tại H có
góc P chung
=>ΔMNP đồng dạng với ΔHIP
b: IN/IP=MN/MP=3/4
=>IN/3=IP/4=(IN+IP)/(3+4)=5/7
=>IN=15/7cm; IP=20/7cm
IH//MN
=>IH/MN=PI/PN
=>IH/3=20/7:5=4/7
=>IH=12/7cm
NX
31 tháng 7 2018
Hình tự vẽ nha :
a)
Ta có : HI \(\perp\)AB => AI \(\perp\)IH
<=> AI là đường cao của tam giác AEH
Mà : EI = IH ( gt )
=> tam giác AEH cân tại A
=> AE = AH
b) chứng minh tương tự như câu (a)
26 tháng 2 2022
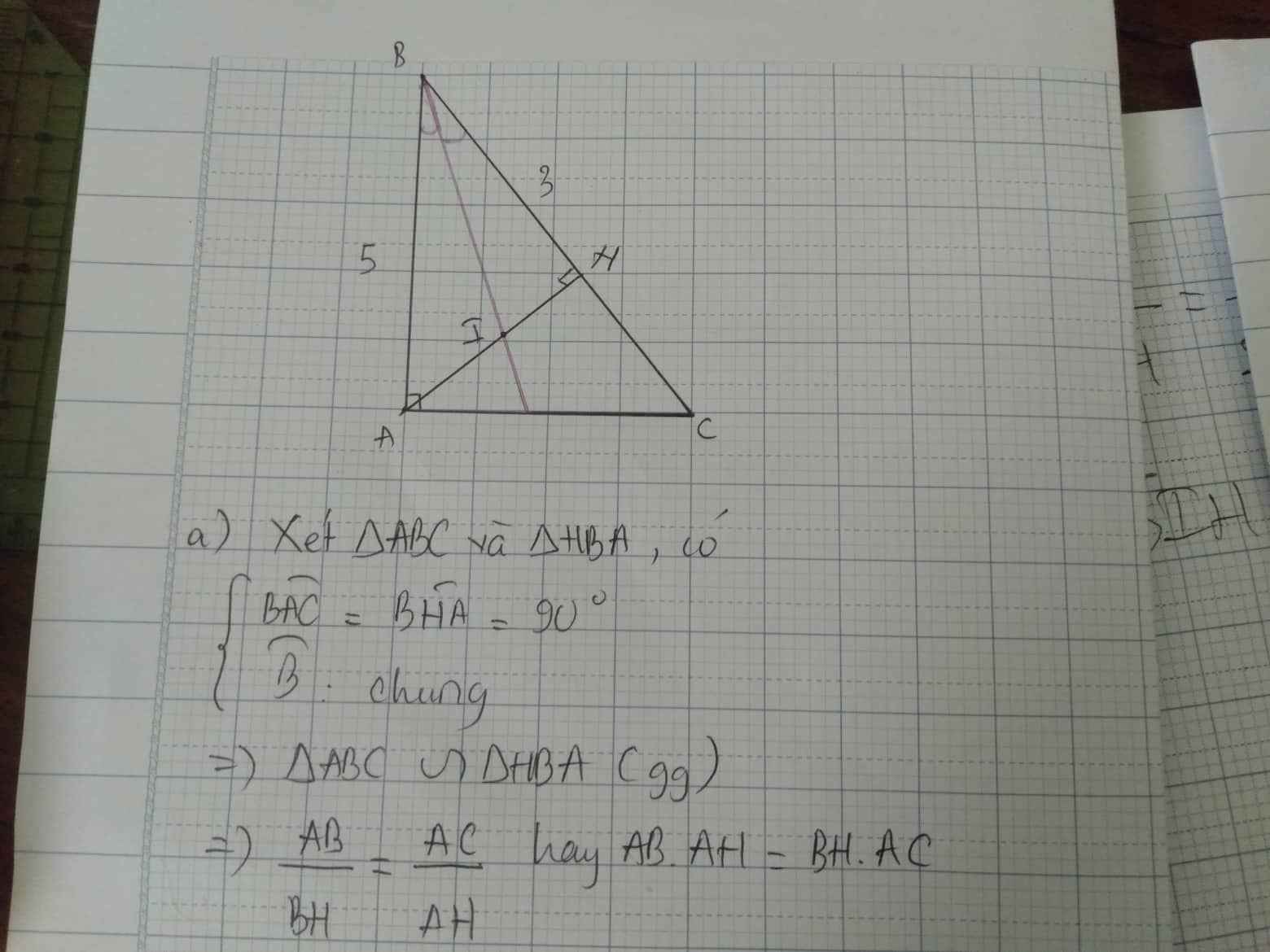
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
=>BH/AB=BC/BA(1)
hay \(AB^2=BH\cdot BC\)
Câu b đề sai rồi bạn
19 tháng 4 2022
a, Ta có △MAB cân tại M => AM=BM(đ/l)=>MI là đường trung trực của AB
=>AI=IB(t/c)
=> góc MAB = góc MBA (đ/l)
Ta có IH vuông góc với AM=> góc IHA=90 độ
Ta có IK vuông góc với MB=> góc IKB = 90 độ
Xét △AHI và △ IBK ta có:
Góc IHA= góc IKB=90 độ(CMT) \
AI=IB(CMT) => △AHI =△ IBK ( cạnh huyền - góc gócMAB=gócMBA(CMT) / nhọn)
b, => IH=IK (2 cạnh tương ứng); => AH=KB (2 cạnh tương ứng)
c, Ta có AM= HM+AH (1)
BM=KM+IK (2)
mà AM=BM (CMT); AH=IK(CMT) (3)
Từ (1), (2), (3) => HM = MK (t/c)
=> △ MHK cân tại M (t/c)
2 tháng 7 2023
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b: Xét ΔCAM có
CK,AH là đường cao
CK cắt AH tại I
=>I là trực tâm
=>MI vuông góc AC
=>MI//AB
Xét ΔHAB có
M là trung điểm của HB
MI//AB
=>I là trung điểm của AH
=>IA=IH
9 tháng 7 2023
a: Xét ΔCAI vuông tại A và ΔCHi vuông tại H có
CI chung
góc ACI=góc HCI
=>ΔCAI=ΔCHI
=>IA=IH
b: IA=IH
IH<IB
=>IA<IB
c: Xét ΔCAB có
K là giao điểm của hai tia phân giác góc ngoài tại đỉnh A,B
=>CK là phân giác của góc ACB
=>C,I,K thẳng hàng
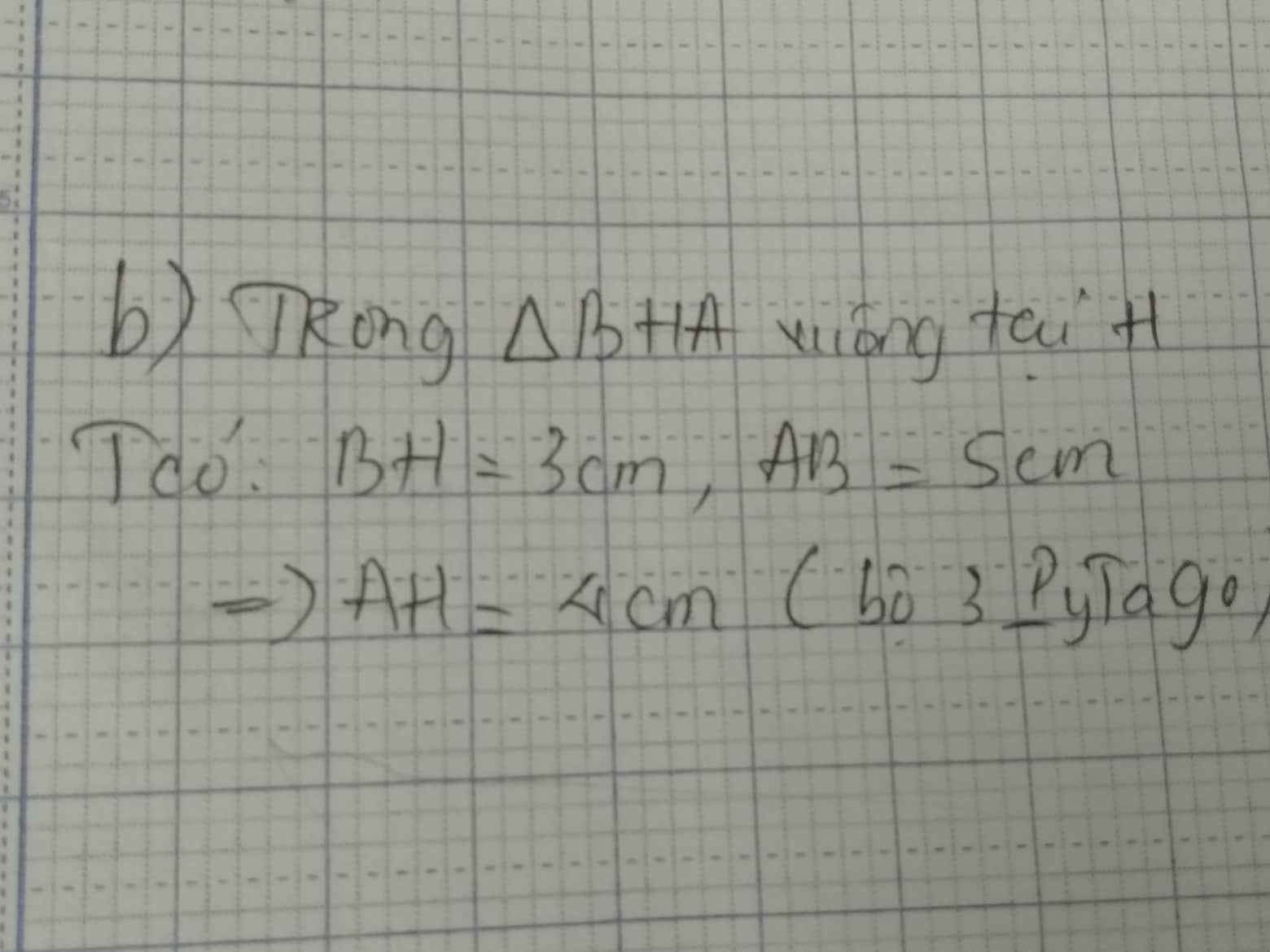
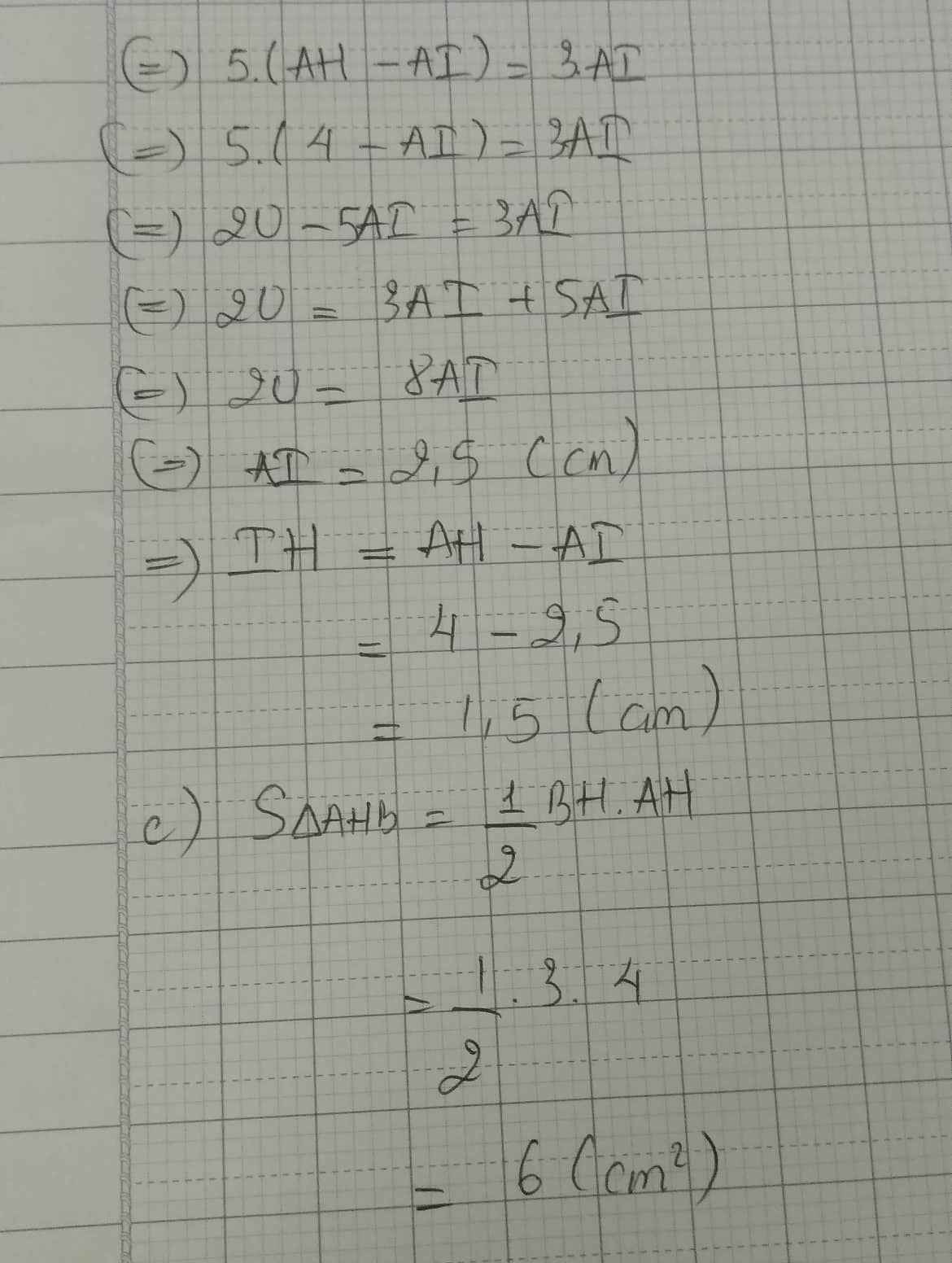
thôi các bn ơi bài kiểm tra tui lm xong lun òi T_T
bằng bao nhiêu vậy