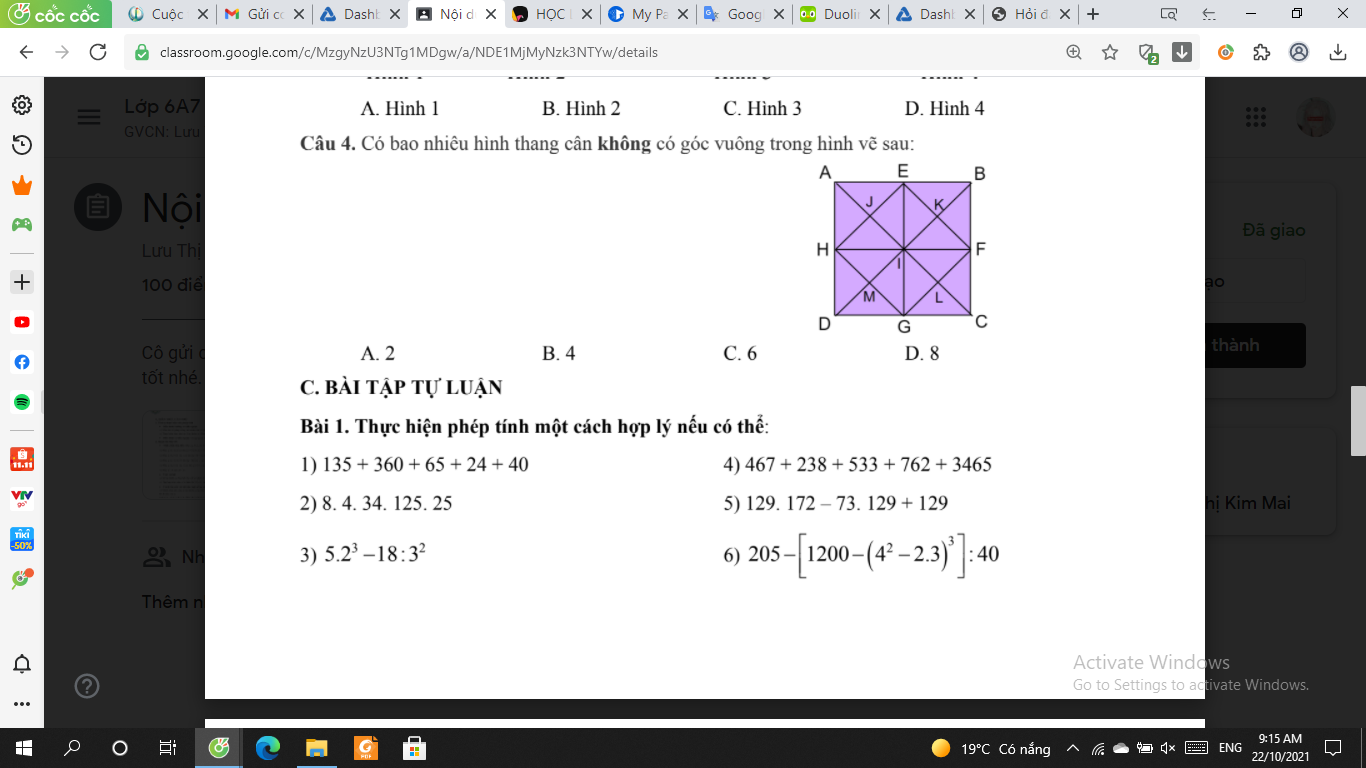
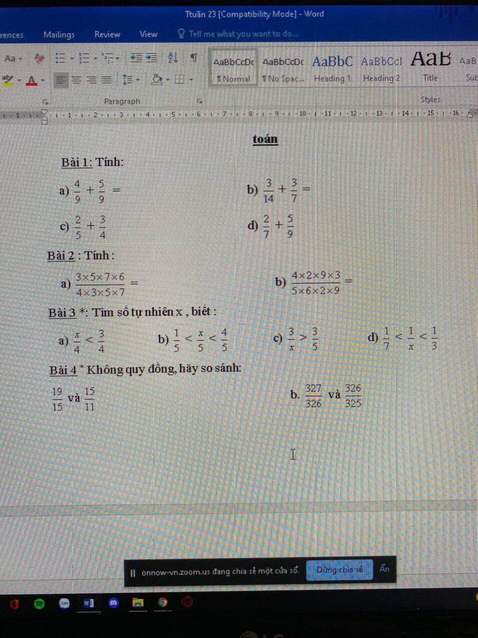 Bài 4 và 1 ạ
Bài 4 và 1 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)


\(\left(\frac{1}{4}-\frac{2}{5}\right):\frac{23}{25}+\left(\frac{3}{4}-\frac{3}{5}\right):\frac{23}{25}\)
\(=\left(\frac{1}{4}-\frac{2}{5}+\frac{3}{4}-\frac{3}{5}\right).\frac{25}{23}\)
\(=-\frac{25}{23}\)

Bài 3.
a. Ta có: \(CK=BK\left(gt\right)\Rightarrow OK\perp BC\)
Ta có: \(\widehat{OIC}=90^o\)
\(\widehat{OKC}=90^o\)
\(\Rightarrow\widehat{OIC}+\widehat{OKC}=90^o+90^o=180^o\)
`=>` Tứ giác CIOK nội tiếp đường tròn
b. Xét \(\Delta AID\) và \(\Delta CIB\), có:
\(\widehat{AID}=\widehat{CIB}=90^o\left(gt\right)\)
\(\widehat{ADI}=\widehat{CBI}\) ( cùng chắn \(\stackrel\frown{AC}\) )
Vậy \(\Delta AID\sim\Delta CIB\) ( g.g)
\(\Rightarrow\dfrac{IA}{IC}=\dfrac{ID}{IB}\)
\(\Leftrightarrow IC.ID=IA.IB\)
c. Kẻ \(DM\perp AC\)
Ta có: \(\widehat{ACB}=90^o\) ( góc nt chắn nửa đtròn )
`->` Tứ giác DMCK là hình chữ nhật
\(\rightarrow DK\perp BC\)
Mà \(OK\perp BC\)
\(\Rightarrow\) 3 điểm D,O,K thẳng hàng

Bài 4:
a: Xét tứ giác ANBH có
M là trung điểm của AB
M là trung điểm của NH
Do đó: ANBH là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên ANBH là hình chữ nhật

e thay dấu = cho tất cả phsố trog bài 3 rồi tìm x , khi tìm x thì coi dấu của bài r nói x lớn hoặc nhỏ hơn số đó là đc

Bài 4:
a: Ta có: \(IA=IB=\dfrac{AB}{2}\)
\(DK=KC=\dfrac{DC}{2}\)
mà AB=DC
nên IA=IB=DK=KC
Xét tứ giác IBKD có
IB//DK
IB=DK
Do đó: IBKD là hình bình hành
b: Xét tứ giác AIKD có
AI//DK
AI=DK
Do đó: AIKD là hình bình hành
Suy ra: Hai đường chéo AK và DI cắt nhau tại trung điểm của mỗi đường
mà AK cắt DI tại E
nên E là trung điểm của DI
Suy ra: \(EI=\dfrac{DI}{2}\left(1\right)\)
Xét tứ giác BIKC có
BI//KC
BI=KC
Do đó: BIKC là hình bình hành
Suy ra: Hai đường chéo IC và BK cắt nhau tại trung điểm của mỗi đường
mà IC cắt BK tại F
nên F là trung điểm của BK
\(\Leftrightarrow KF=\dfrac{BK}{2}\left(2\right)\)
Ta có: IBKD là hình bình hành
nên \(ID=BK\left(3\right)\) và ID=BK
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra EI//KF và EI=KF
Xét tứ giác IEKF có
IE//KF
IE=KF
Do đó: IEKF là hình bình hành
Bài 4:
c: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
Suy ra: Hai đường chéo AC và IK cắt nhau tại trung điểm của mỗi đường\(\left(4\right)\)
Ta có: EIFK là hình bình hành
nên hai đường chéo EF và IK cắt nhau tại trung điểm của mỗi đường\(\left(5\right)\)
Từ \(\left(4\right),\left(5\right)\) suy ra AC,EF,IK đồng quy
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn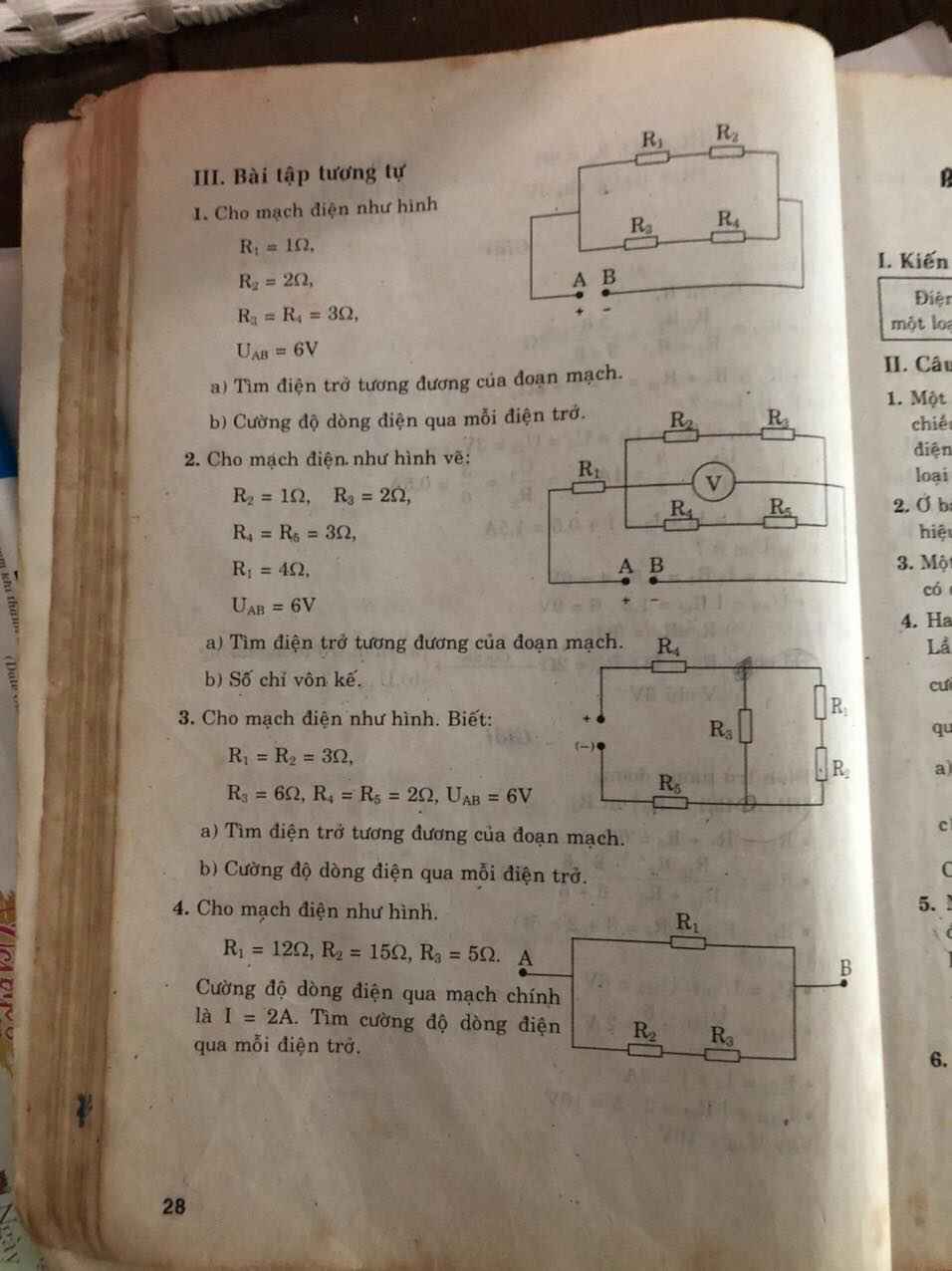

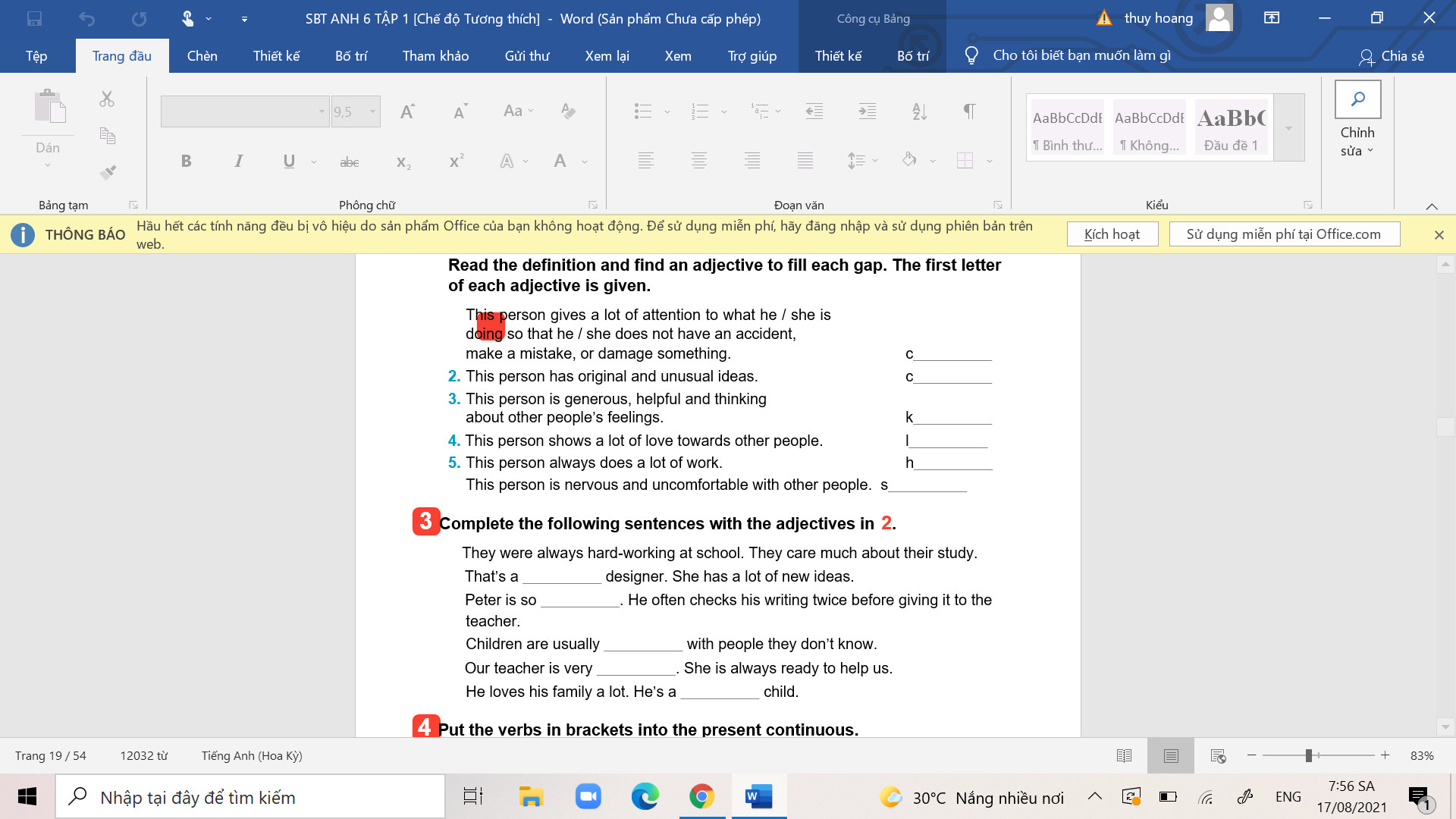 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3. các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé.