x6-x4+2x2+2x3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(=\left(x^6+2x^5+x^4\right)-2\left(x^5+2x^4+x^3\right)+2\left(x^4+2x^3+x^2\right)\)
\(=x^2\left(x^2+x\right)^2-2x\left(x^2+x\right)^2+2\left(x^2+x\right)^2\)
\(=\left(x^2+x\right)^2\left(x^2-2x+2\right)\)
\(=x^2\left(x+1\right)^2\left(x^2-2x+2\right)\)

a) x6 – x4 + 2x3 + 2x2
= x2(x4 – x2 + 2x + 2)
= x2[x2(x2 – 1) + 2(x + 1)]
= x2. [x2.(x -1).(x + 1) + 2(x+ 1)]
= x2 (x+ 1).[x2(x- 1)+ 2]
= x2(x + 1)(x3 – x2 + 2)
= x2(x + 1)[(x3 + 1) – (x2 – 1)]
= x2(x + 1).[(x + 1).(x2 – x + 1) - (x - 1).(x + 1)]
= x2(x + 1)(x + 1)( x2 – x + 1 – x + 1)
= x2(x + 1)2(x2 – 2x + 2).
b) 4x4 + y4 = 4x4 + 4x2y2 + y4 - 4x2y2
= (2x2 + y2)2 - (2xy)2
= (2x2 + y2 + 2xy)(2x2 + y2 - 2xy)

Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
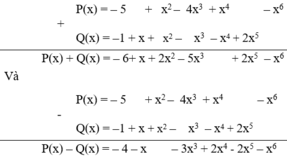
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6

P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
= – x6 + x4 + (– 3x3 – x3) + (3x2 – 2x2) – 5
= – x6 + x4 – 4x3 + x2 – 5.
= – 5+ x2 – 4x3 + x4 – x6
Và Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1
= 2x5 – x4 + (x3 – 2x3) + x2 + x –1
= 2x5 – x4 – x3 + x2 + x –1.
= –1+ x + x2 – x3 – x4 + 2x5

a) (x - y)(x + y + 3). b) (x + y - 2xy)(2 + y + 2xy).
c) x 2 (x + l)( x 3 - x 2 + 2). d) (x – 1 - y)[ ( x - 1 ) 2 + ( x - 1 ) y + y 2 ].

a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

a: Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x-1\right)^3\cdot\left(x+1\right)\)
b: Ta có: \(-a^4+a^3+2a^3+2a^2\)
\(=-a^2\left(a^2-a-2a-2\right)\)
c: Ta có: \(x^4+x^3+2x^2+x+1\)
\(=x^4+x^3+x^2+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^2+1\right)\)