Ba ngọn hải đăng phát ra ba dấu hiệu khác nhau. Hai dấu hiệu liên tiếp của hải đăng
A cách nhau 16 giây, hải đăng B cách nhau 45 giây và hải đăng C là 150 giây. Đúng 18 giờ
cả 3 dấu hiệu cùng phát ra một lúc. Hỏi lúc mấy giờ cả ba dấu hiệu lại cùng phát ra một lúc
sau đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BCNN(16, 45,150)= 3600
=> Sau 3600 giây = 1 giờ nữa thì ba dấu hiệu lại cùng phát ra
Vậy lúc 19 giờ thì cả ba dấu hiệu cùng phát ra một lúc
Gọi a là giờ cả 3 dấu hiệu của 3 ngọn hải đăng phát ra.( a = giây)
Sau a giây, cả 3 ngọn hải đăng đều phát ra dấu hiệu. nên a chia hết cho 16 giây, 45 giây và 150 giây.
Vì đề bài hỏi giờ mà cả 3 dấu hiệu xuất hiện cùng lúc sau đợt thứ nhất xuất hiện, nên ta tìm số nhỏ nhất chia hết cho 16, 45, 150.
Vậy số nhỏ nhất chia hết cho 16, 45, 150 là: 3600(giây), 3600 giây = 60 phút = 1 giờ
Cả 3 dấu hiệu cùng phát ra một lúc tại:
18 giờ + 1 giờ = 19 giờ
Đáp số : 19 giờ

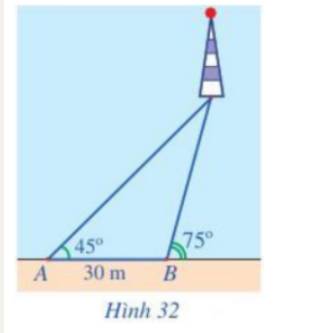
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
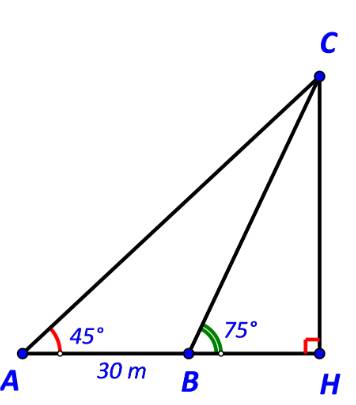
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.
Gọi a là giờ cả 3 dấu hiệu của 3 ngọn hải đăng phát ra.( a = giây)
Sau a giây, cả 3 ngọn hải đăng đều phát ra dấu hiệu. nên a chia hết cho 16 giây, 45 giây và 150 giây.
Vì đề bài hỏi giờ mà cả 3 dấu hiệu xuất hiện cùng lúc sau đợt thứ nhất xuất hiện, nên ta tìm số nhỏ nhất chia hết cho 16, 45, 150.
Vậy số nhỏ nhất chia hết cho 16, 45, 150 là: 3600(giây), 3600 giây = 60 phút = 1 giờ
Cả 3 dấu hiệu cùng phát ra một lúc tại:
18 giờ + 1 giờ = 19 giờ
Đáp số : 19 giờ