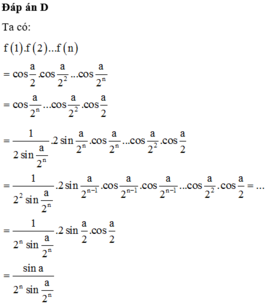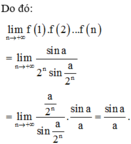Cho đa giác đều A 1A 2......A2n,n (n≥2 ; n∈Z) nội tiếp trong đường tròn (O). Tính:
a. Số đoạn thẳng mà hai đầu mút là hai trong 2n đỉnh A1, A 2,....A2n ?
b. Số vectơ khác vectơ – không mà điểm đầu và điểm cuối của chúng là hai trong 2n đỉnh
A1, A 2,.......A2n ?
c. Số đường chéo của đa giác trên?
d. Số tam giác có các đỉnh là ba trong 2n đỉnh A1, A2,.....A2n ?
e. Số hình chữ nhật có các đỉnh là bốn trong 2n đỉnh A1, A2,........A2n ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: ![]()
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng ![]()
Theo giả thiết: ![]()
⇒n=8.
Chọn C

a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)

Đáp án B
Đa giác đều 2n đỉnh có n đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng với 1 hình chữ nhật ⇒ C n 2 = 45 ⇔ n = 10