4a2:(a+3) =1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án đúng : A
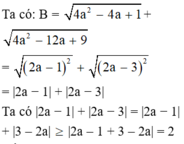
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2

Số hs nam là \(28\times\left(1-\dfrac{3}{7}\right)=16\left(hs\right)\)
Số hs nam là 28×(1−\(\dfrac{\text{3}}{\text{7}}\))=16(hs)
Đáp số:16 HS
HT nha

Vì a
≠
±
3/2 nên
4
a
2
-
9
≠
0 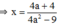
Vì a
≠
- 1 nên
3
a
3
+
3
≠
0 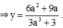
Do đó: 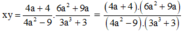
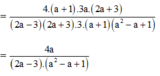

số học sinh nam là :
(55 + 3) : 2 = 29 (học sinh)
số học sinh nữ là:
29 - 3 = 26 (học sinh)
đ\s_
Số h/s nam của lớp 4A2 là:
(55+3):2=44
Số h/s nữ của lớp 4A2 là:
55-44=11
Đáp số:h/s nam:44
h/s nữ :11

\(a,=\left(x+1\right)\left(x+3\right)\\ b,=-5x^2+15x+x-3=\left(x-3\right)\left(1-5x\right)\\ c,=2x^2+2x+5x+5=\left(2x+5\right)\left(x+1\right)\\ d,=2x^2-2x+5x-5=\left(x-1\right)\left(2x+5\right)\\ e,=x^3+x^2-4x^2-4x+x+1=\left(x+1\right)\left(x^2-4x+1\right)\\ f,=x^2+x-5x-5=\left(x+1\right)\left(x-5\right)\)

Áp dụng BĐT \(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(a+c-b\right)\)
\(\Leftrightarrow abc\ge\left(3-2a\right)\left(3-2b\right)\left(3-2c\right)\ge0\)
\(\Leftrightarrow9abc+18\left(a+b+c\right)\ge12\left(ab+bc+ca\right)+27\)
\(\Leftrightarrow abc\ge\dfrac{4}{3}\left(ab+bc+ca\right)-3\)
Do đó:
\(P=4a^2+4b^2+4c^2+abc\ge4a^2+4b^2+4c^2+\dfrac{4}{3}\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{2}{3}\left(a+b+c\right)^2+\dfrac{10}{3}\left(a^2+b^2+c^2\right)-3\)
\(P\ge\dfrac{2}{3}\left(a+b+c\right)^2+\dfrac{10}{9}\left(a+b+c\right)^2-3=13\)
Đề bài bạn viết thiếu số 1 bên vế phải rồi
Lời giải:
Áp dụng BĐT Schur:
$abc\geq (a+b-c)(b+c-a)(c+a-b)=(3-2a)(3-2b)(3-2c)$
$\Leftrightarrow 9abc\geq 12(ab+bc+ac)-27$
$\Leftrightarrow abc\geq \frac{4}{3}(ab+bc+ac)-3$
Do đó:
$4(a^2+b^2+c^2)+abc\geq 4(a^2+b^2+c^2)+\frac{4}{3}(ab+bc+ac)-3$
$=\frac{10}{3}(a^2+b^2+c^2)+\frac{2}{3}(a+b+c)^2-3$
$\geq \frac{10}{9}(a+b+c)^2+\frac{2}{3}(a+b+c)^2-3=13$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=1$
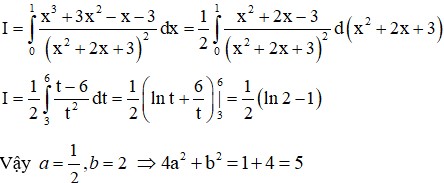
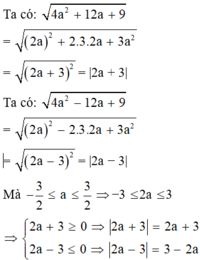
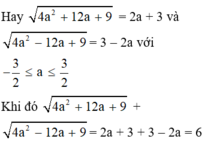
4a^2 : (a+3)=1
=>a+3=4a2 : 1
a+3=4a.a
<=> 4a.a - a-3=0
a.(4a-1)-3=0
=>a.(4a-1)=3
=>a và 4a-1 thuộc Ư(3)={1;-1;3;-3}
với a =1=>4a-1=3<=>a=1(tm)
với a=-1=>4a-1=-3<=>a=-1/2(ktm)
với a=3=>4a-1=1<=>a=1/2(ktm)
với a= -3=>4a-1=-1<=>a=0(ktm)
vậy ....