Limx➞+-∞ {(x-1)2(7x+2)2}/(2x+1)4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\lim\limits_{x\rightarrow\infty}\left(\sqrt{x+1}-\sqrt{x}\right)=\lim\limits_{x\rightarrow\infty}\dfrac{1}{\sqrt{x+1}+\sqrt{x}}=\dfrac{1}{\infty}=0\).
a) \(lim_{x\rightarrow+\infty}\left(\sqrt{x+1}-\sqrt{x}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{x+1}+\sqrt{x}}\right)=0\)
b) \(lim_{x\rightarrow+\infty}\left(\sqrt{x+\sqrt{x}}-\sqrt{x}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{x+\sqrt{x}-x}{\sqrt{x+\sqrt{x}}+\sqrt{x}}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{\sqrt{x}}{\sqrt{x+\sqrt{x}}+\sqrt{x}}\right)\)
\(=lim_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{\dfrac{x+\sqrt{x}}{x}}+1}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{1+\dfrac{1}{\sqrt{x}}}+1}\right)=\dfrac{1}{2}\)
c) \(lim_{x\rightarrow-\infty}\left(\sqrt{3x^2+x+1}+x\sqrt{3}\right)=lim_{x\rightarrow-\infty}\left(\dfrac{x+1}{\sqrt{3x^2+x+1}-x\sqrt{3}}\right)\)
\(=lim_{x\rightarrow-\infty}\left(\dfrac{1+\dfrac{1}{x}}{\sqrt{\dfrac{3x^2+x+1}{x^2}}-\dfrac{x\sqrt{3}}{x^2}}\right)\)
\(=lim_{x\rightarrow-\infty}\left(\dfrac{1+\dfrac{1}{x}}{\sqrt{3+\dfrac{1}{x}+\dfrac{1}{x^2}}-\dfrac{\sqrt{3}}{x}}\right)=\dfrac{1}{\sqrt{3}}\)
d) \(lim_{x\rightarrow+\infty}\left(\sqrt{x^2+2x+4}-\sqrt{x^2-2x+4}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{4x}{\sqrt{x^2+2x+4}+\sqrt{x^2-2x+4}}\right)\)
\(=lim_{x\rightarrow+\infty}\left(\dfrac{4}{\sqrt{1+\dfrac{2}{x}+\dfrac{4}{x^2}}+\sqrt{1-\dfrac{2}{x}+\dfrac{4}{x^2}}}\right)=\dfrac{4}{2}=2\)

a. Áp dụng công thức L'Hospital:
\(\lim\limits_{x\to 0}\frac{\sqrt{x+1}-\sqrt{1-x}}{\sqrt[3]{x+1}-\sqrt{1-x}}=\lim\limits_{x\to 0}\frac{\frac{1}{2}(x+1)^{\frac{-1}{2}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}{\frac{1}{3}(x+1)^{\frac{-2}{3}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}=\frac{1}{\frac{5}{6}}=\frac{6}{5}\)
b.
\(\lim\limits_{x\to 0}(\frac{1}{x}-\frac{1}{x^2})=\lim\limits_{x\to 0}\frac{x-1}{x^2}=-\infty\)
c. Áp dụng quy tắc L'Hospital:
\(\lim\limits_{x\to +\infty}\frac{x^4-x^3+11}{2x-7}=\lim\limits_{x\to +\infty}\frac{4x^3-3x^2}{2}=+\infty \)
d.
\(\lim\limits_{x\to 5}\frac{7}{(x-1)^2}.\frac{2x+1}{2x-3}=\frac{7}{(5-1)^2}.\frac{2.5+11}{2.5-3}=\frac{11}{16}\)

a/ \(=\lim\limits_{x\rightarrow\pm\infty}\dfrac{\dfrac{\left(2x\right)^2.\left(4x\right)^3}{x^4}}{\dfrac{\left(3x\right)^2\left(5x^2\right)}{x^4}}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{4^4.x}{45}=\pm\infty\)
b/ \(=\lim\limits_{x\rightarrow\pm\infty}\dfrac{\sqrt[3]{\dfrac{x^3}{x^3}+\dfrac{2x^2}{x^3}+\dfrac{x}{x^3}}}{\dfrac{2x}{x}-\dfrac{2}{x}}=\dfrac{1}{2}\)
c/ \(=\lim\limits_{x\rightarrow\pm\infty}\dfrac{\dfrac{\sqrt[3]{\left(x^3+2x^2\right)^2}}{x^2}+\dfrac{x\sqrt[3]{x^3+2x^2}}{x^2}+\dfrac{x^2}{x^2}}{\dfrac{3x^2}{x^2}-\dfrac{2x}{x^2}}=\dfrac{1+1+1}{3}=1\)
d/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{\left(-3x\right)^3x^2}{x^5}}{-\dfrac{4x^5}{x^5}}=\dfrac{-27}{-4}=\dfrac{27}{4}\)
e/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{\left(2x\right)^{20}.\left(3x\right)^{20}}{x^{50}}}{\dfrac{\left(2x\right)^{50}}{x^{50}}}=0\)
g/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{8x^3.\left(4x^5\right)^9}{x^{47}}}{\dfrac{11x^{47}}{x^{47}}}=+\infty\)

\(A=\lim\limits_{x\rightarrow2}\frac{\left(x-2\right)\left(2x-1\right)}{x-2}=\lim\limits_{x\rightarrow2}\left(2x-1\right)=3\)
\(B=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2-2x+3\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x^2-2x+3}{x+1}=\frac{1-2+3}{1+1}=1\)
\(C=\lim\limits_{x\rightarrow2}\frac{x^2+2x}{x^2+4x+4}=\frac{4+4}{4+8+4}=\frac{1}{2}\)
\(D=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2-1\right)}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow1}\frac{x^2-1}{x-2}=\frac{0}{-1}=0\)
\(E=\lim\limits_{x\rightarrow1}\frac{x^3-5x^2+3x+9}{x^4-8x^4-9}=\frac{1-5+3+9}{1-8-9}=-\frac{1}{2}\)
\(F=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x-1\right)\left(x^2+1\right)}{\left(x+1\right)\left(x^2-3x+3\right)}=\lim\limits_{x\rightarrow-1}\frac{\left(x-1\right)\left(x^2+1\right)}{x^2-3x+3}=\frac{-2.2}{1+3+3}=-\frac{2}{5}\)
\(G=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(2x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x+3}{2x+1}=\frac{4}{3}\)
\(H=\lim\limits_{x\rightarrow-2}\frac{\left(x+2\right)\left(x-1\right)^2}{\left(2-x\right)\left(x+2\right)}=\lim\limits_{x\rightarrow-2}\frac{\left(x-1\right)^2}{2-x}=\frac{9}{4}\)
\(I=\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+1}{x^2-1}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4}{2x}=\frac{24-25}{2}=-\frac{1}{2}\)
\(K=\lim\limits_{x\rightarrow1}\frac{x^m-1}{x^n-1}=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)

\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+\sqrt{x^2+2}}{\sqrt{8x^2+5x+2}}=\dfrac{1+\sqrt{1+\dfrac{2}{x^2}}}{\sqrt{8+\dfrac{5}{x}+\dfrac{2}{x^2}}}=\dfrac{1+\sqrt{1}}{\sqrt{8}}=\dfrac{\sqrt{2}}{2}\).
Thiếu \(\lim\limits_{x\rightarrow-\infty}\) ở sau dấu bằng thứ nhất nha

\(\frac{x+1}{x-2}+\frac{x-1}{x+2}=\frac{2\left(x^2+2\right)}{x^2-4}\left(x\ne\pm2\right)\)
\(\Leftrightarrow\frac{\left(x+1\right)\left(x+2\right)+\left(x-1\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{2\left(x^2+2\right)}{x^2-4}\)
\(\Leftrightarrow\frac{2x^2+4}{x^2-4}=\frac{2x^2+4}{x^2-4}\)
Vậy phương trình này có vô số nghiệm x thỏa mãn trừ x khác 2 và -2

f: Ta có: \(16x^2-9\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(4x-3x-3\right)\left(4x+3x+3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(7x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{7}\end{matrix}\right.\)

b)
ĐKXĐ: \(x\notin\left\{2;3;\dfrac{1}{2}\right\}\)
Ta có: \(\dfrac{x+4}{2x^2-5x+2}+\dfrac{x+1}{2x^2-7x+3}=\dfrac{2x+5}{2x^2-7x+3}\)
\(\Leftrightarrow\dfrac{x+4}{\left(x-2\right)\left(2x-1\right)}+\dfrac{x+1}{\left(x-3\right)\left(2x-1\right)}=\dfrac{2x+5}{\left(2x-1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-2\right)\left(2x-1\right)\left(x-3\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1\right)}=\dfrac{\left(2x+5\right)\left(x-2\right)}{\left(2x-1\right)\left(x-3\right)\left(x-2\right)}\)
Suy ra: \(x^2-3x+4x-12+x^2-2x+x-2=2x^2-4x+5x-10\)
\(\Leftrightarrow2x^2-14=2x^2+x-10\)
\(\Leftrightarrow2x^2-14-2x^2-x+10=0\)
\(\Leftrightarrow-x-4=0\)
\(\Leftrightarrow-x=4\)
hay x=-4(nhận)
Vậy: S={-4}
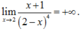
\(\lim\limits_{x\rightarrow\infty}\frac{\left(x-1\right)^2\left(7x+2\right)^2}{\left(2x+1\right)^4}=\lim\limits_{x\rightarrow\infty}\frac{x^2\left(1-\frac{1}{x}\right)^2.x^2\left(7+\frac{2}{x}\right)^2}{x^4\left(2+\frac{1}{x}\right)^4}=\frac{1.7^2}{2^4}=\frac{49}{16}\)