Giúp e với ạ=3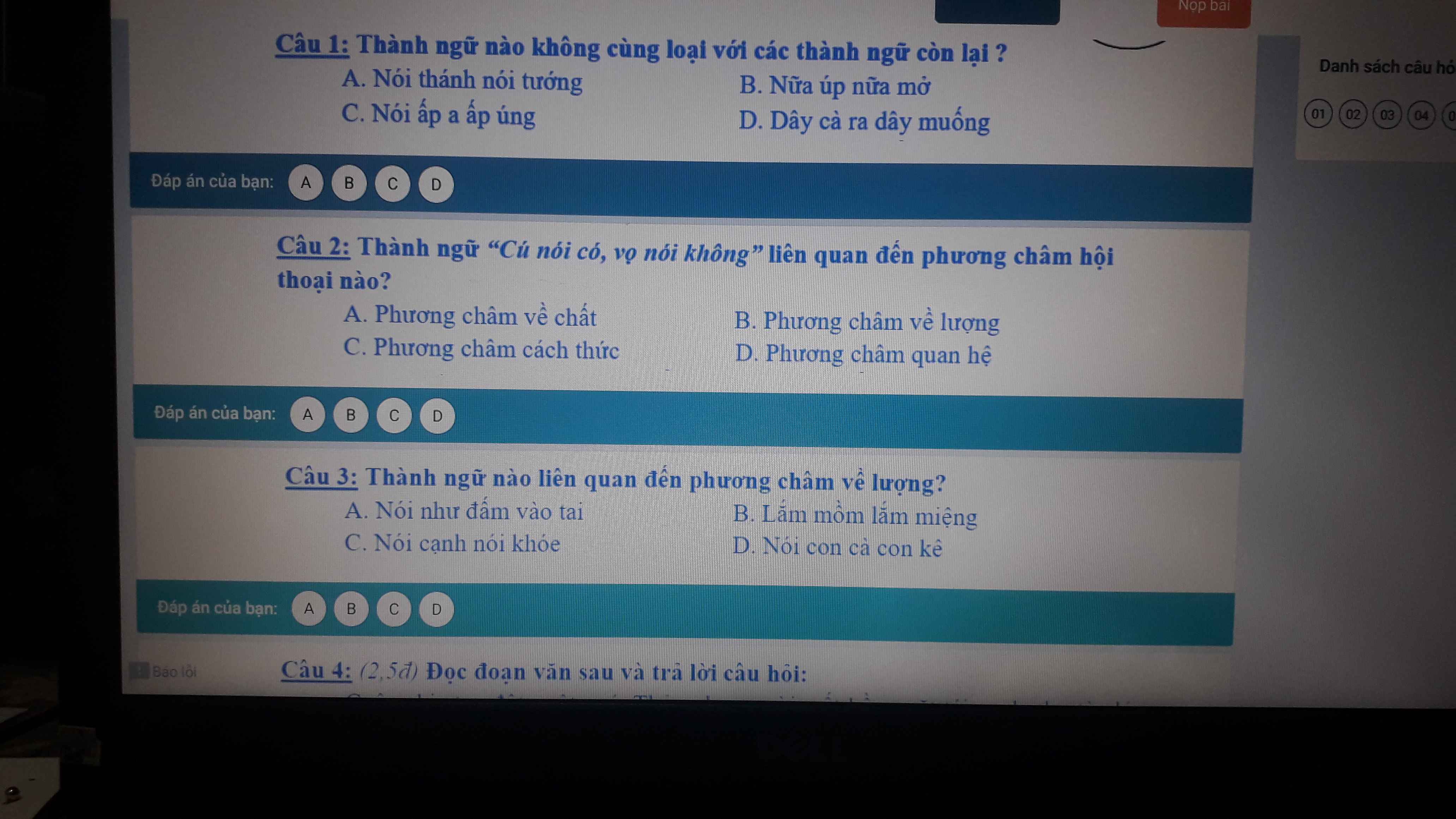

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(sin\left(\dfrac{\pi}{2}-x\right)+cot^2x=cosx+\dfrac{cos^2x}{sin^2x}=cosx+\dfrac{cos^2x}{1-cos^2x}=a+\dfrac{a^2}{1-a^2}\)
\(=\dfrac{-a^3+a^2+a}{1-a^2}\)
\(\Rightarrow\left\{{}\begin{matrix}m=-1\\n=1\\\end{matrix}\right.\) \(\Rightarrow P=-3\)

Tóm tắt:
\(k=10\)N/m, \(m=1kg\), \(g=10m\)/s2
a)\(\Delta l=?\)
b)\(l'=2cm=0,02m\)
\(W_{tt}=?;W_{đh}=?;W=?\)
Giải chi tiết:
a)Lực đàn hồi: \(F=P\Rightarrow k\cdot\Delta l=mg\)
\(\Rightarrow\Delta l=\dfrac{mg}{k}=\dfrac{1\cdot10}{10}=1cm\)
b)Thế năng trọng trường:
\(W_{tt}=?\) do không có cách nào ra đc kết quả kia


\(cos\left(\dfrac{\pi}{2}-x\right)+tan^2x=sinx+\dfrac{sin^2x}{cos^2x}=sinx+\dfrac{sin^2x}{1-cos^2x}\)
\(=a+\dfrac{a^2}{1-a^2}=\dfrac{-a^3+a^2+a}{1-a^2}\Rightarrow\left\{{}\begin{matrix}m=-1\\n=1\end{matrix}\right.\)
\(\Rightarrow Q=-4\)


B.
Có khái niệm trong SGK ghi rất rõ, em có thể tham khảo thêm

3.
\(\overrightarrow{AB}=\left(4;2\right)=2\left(2;1\right)\)
Do đó đường thẳng AB nhận \(\left(-1;2\right)\) là 1 vtpt
4.
\(\overrightarrow{AB}=\left(-a;b\right)\)
\(\Rightarrow\) Đường thẳng AB nhận (b;a) là 1 vtpt









