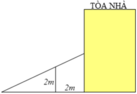
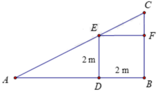
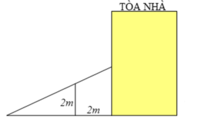
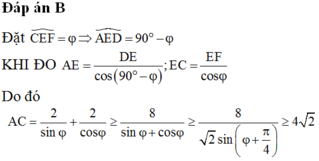
bài 1 : gần nhà bạn Tòa có 1 bức tường rào xung quanh nhà . để trèo lên bức tường bạn Tòa đã dùng 1 chiếc thang đặt tường . biết rằng chiều dài của cầu thang là 5m và chân thang cách tường là 3m . hãy tính chiều cao của bức tường
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 4 2020
( Hình ảnh chỉ có tính chất minh họa )
Áp dụng định lý Pytago vào tam giác ABC, ta có:
AB2 + AC2 = BC2
=> AB2 + 32 = 52
=> AB2 + 9 = 25
=> AB2 = 25 - 9
=> AB2 = 16
=> AB = 4m
nhớ tk cho mk nha
3 tháng 5 2020
bạn bị hâm à?đến bạn còn trả biết làm mà bạn đi bảo mình làm là sao? hỏi bạn khác đi.
7 tháng 3 2022
Do chiếc thang đang dựa vào tòa nhà
mà chân tòa nhà là chân đường vuông góc
=>hình dáng mà chiếc thang cùng với tòa nhà tạo thành là hình tam giác vuông
áp dụng định lí pi-ta-go, ta có:
52+202=425
=>425=20.62(mình đã làm tròn con số đến số đầu tiên của phần thập phân số gốc là 20.6155281280883)
Vậy chiếc thang dài \(\approx\)20,6 m
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
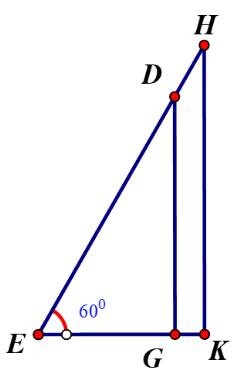
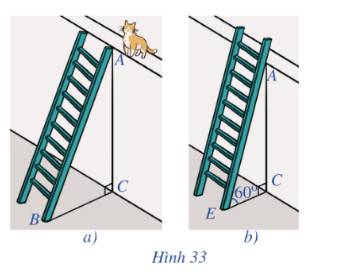
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.
9 tháng 3 2021
Gọi chiếc thang có cạnh AB, chân thang đến chân tường có cạnh BC, chân tường đến đầu chiếc thang là AC.
Xét ΔABC vuông tại C có:
CA2+CB2=AB2CA2+CB2=AB2 (Định lý Pi-ta-go)
CA2+52=132CA2+52=132
CA2=169−25CA2=169-25
CA2=144CA2=144
⇒ CA=12 m
H9
HT.Phong (9A5)
CTVHS
3 tháng 8 2023
Gọi tam giác tạo thành là tam giác ABC
Với chiếc thang là cạnh huyền AC, khoảng cách của chân thang và chân tường là BC và chiều cao của bức tường là AB:
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{1,5^2+6^2}\approx6,2\left(m\right)\)
Độ dài của chiếc thang nhỏ:
\(A'C'=\dfrac{2}{3}\cdot AC=\dfrac{2}{3}\cdot6,2\approx4,13\left(m\right)\)
Áp dụng định lý Py-ta-go ta tìm được độ cao mà thang đặt đến:
\(A'B'=\sqrt{A'C'^2-B'C'^2}=\sqrt{4,13^2-1^2}\approx4\left(m\right)\)
Điểm cao nhất của thang cách mặt bước tường là:
\(AB-A'B'=6-4=2\left(m\right)\)
Vậy....