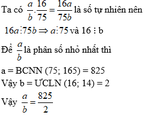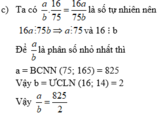Tìm phân số tối giản a/b nhỏ nhất (a, b thuộc N*) để khi a/b nhân với các phân số 14/75, 21/100 được mỗi tích là số tự nhiên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
10 tháng 4 2017
a) ta có: 8/11 =(8+a)/(11+55)
<=> 66x8=11(8+a)
<=> 528=88+11a
<=> 11a=440
=> a=440:11=40
=> để phân số không đổi ta phải thêm vào tử 40 đơn vị. Phân số mới là: 48/66
b) để a/b nhân với 2 phân số đó tích là số tự nhiên thì a phải chia hết cho 75; 165 và b phải chia hết cho 16; 14.
BSCNN của 75, 165 là: 5x5x3x11=825 => a=825
BSCNN của 16, 14 là 7x16=112 => b=112
Phân số cần tìm là: 825/112
8 tháng 5 2016
Ta có \(\frac{a}{b}\)*\(\frac{15}{32}\)=\(\frac{15a}{32b}\)
Mà ƯCLN(15;32)=1=>a\(⋮\)32;15\(⋮\)b(1)
\(\frac{a}{b}\)*\(\frac{25}{24}\)=\(\frac{25a}{24b}\)
Mà ƯCLN(24;25)=1=>a\(⋮\)24;25\(⋮\)b(2)
Từ (1) và (2)=>aEBC(24;32);bEƯC(25;15)
Mà \(\frac{a}{b}\) là phân số nhỏ nhất
=>aEBCNN(24;32);bEƯCLN(25;15)
=>a=96;b=5
Vậy phân số cần tìm là:\(\frac{96}{5}\)
