Cho góc bẹt xOy. Các tia Oa, Ob thuộc cùng một nửa mặt phẳng bờ xy. Trên hình vẽ có bao nhiêu góc ? Hãy kể tên các góc đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 12 2017
Có 10 góc, đó là các góc x O a , x O b , x O c , x O y , a O b , a O c , a O y , b O c , b O y , c O y
NA
6 tháng 3 2020
Ta có: Cứ 2 tia tạo thành 1 góc
=> Số góc tạo bởi 5 tia Oa,Ob,Oc,Ox là :
\(\frac{5x4}{2}\)= 10 (góc)
Vậy các góc đó là: góc xOa, góc aOb, góc bOc, góc cOy, góc xOy
Hok tốt!
Lạc
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
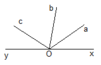
Ta có : Cứ 2 tia tạo thành 1 góc .
\(\Rightarrow\) Số góc tạo bởi 5 tia Oa , Ob , Oc , Ox , Oy là :
\(\frac{5\times4}{2}=10\)( góc )
Vậy các góc đó là : góc xOa , góc aOb , góc bOc , góc cOy , góc xOy .
bạn ơi bạn có thể vẽ lại hình cho mình đc ko