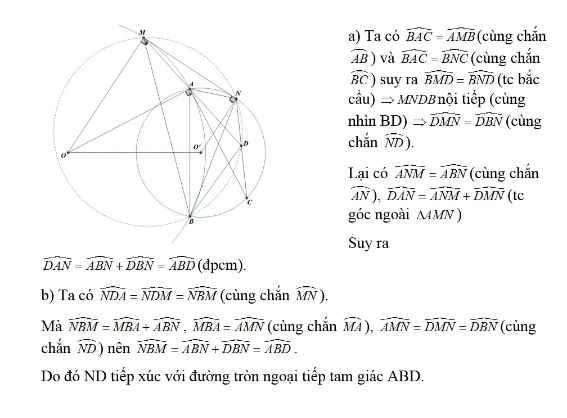
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ tiếp tuyến chung MN của (O) và (O') với \(M\in\left(O\right), N\in\left(O'\right)\)và A nằm trong tam giác BMN. Tiếp tuyến tại A của (O) cắt (O') C, MA cắT NC tại D. Chứng minh rằng:
a) \(\widehat{NAD}=\widehat{ABD}\)
b) ND tiếp xúc với đường tròn ngoại tiếp \(\Delta ABD\)