Phương trình x^3 + x = 0 có mấy nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3.
Đặt \(f\left(x\right)=x^4-3x^3+x-\dfrac{1}{8}\)
Hàm \(f\left(x\right)\) liên tục trên R
Do \(f\left(x\right)\) là đa thức bậc 4 nên có tối đa 4 nghiệm
Ta có: \(f\left(-1\right)=\dfrac{23}{8}>0\)
\(f\left(0\right)=-\dfrac{1}{8}< 0\Rightarrow f\left(-1\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(f\left(\dfrac{1}{2}\right)=\dfrac{1}{16}>0\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\)
\(f\left(1\right)=-\dfrac{9}{8}< 0\Rightarrow f\left(\dfrac{1}{2}\right).f\left(1\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(\dfrac{1}{2};1\right)\)
\(f\left(3\right)=\dfrac{23}{8}>0\Rightarrow f\left(1\right).f\left(3\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;3\right)\)
Vậy pt có 4 nghiệm thuộc các khoảng nói trên
4.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+ax+2017}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{ax+2017}{\sqrt{x^2+ax+2017}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{2017}{x}}{-\sqrt{1+\dfrac{a}{x}+\dfrac{2017}{x^2}}-1}=-\dfrac{a}{2}\)
\(\Rightarrow-\dfrac{a}{2}=6\Rightarrow a=-12\)

a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 

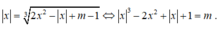
Đồ thị hàm số y = | x | 3 - 2 x 2 + | x | + 1 có dạng như hình (2)
Số nghiệm của phương trình | x | 3 - 2 x 2 + | x | + 1 = m là số giao điểm của đồ thị hàm số y = | x | 3 - 2 x 2 + | x | + 1 và đường thẳng y = m.
Số nghiệm của phương trình y = | x | 3 - 2 x 2 + | x | + 1 là số giao điểm của đồ thị hàm số và đường thẳng y = m.
Dựa vào đồ thị với m > 0 phương trình có tối thiểu 0 nghiệm ( 0 nghiệm – tức là phương trình vô nghiệm).
Chọn A

Bước 1: Tìm \(\Delta\)và rút gọn
Bước 2: Để pt .. <=> \(\Delta\).. 0
Bước 3: Kết luận
Chúc bạn thành công =))))))

a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)
=>4m=-13
hay m=-13/4
c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)
=>-8m>=-4
hay m<=1/2

Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ó x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ó x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ó x < 3
Phương trình đã cho trở thanh 3 – x = 1 ó x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ó x – 1 = 0 ó x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Đáp án cần chọn là: B

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
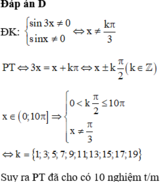
\(x^3+x=0\)
\(x\left(x^2+1\right)=0\)
\(\orbr{\begin{cases}x=0\\x^2+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x^2=-1\left(l\right)\end{cases}}}\)
Vậy pt \(x^3+x=0\)có nghiệm duy nhất là x=0